Exercícios Resolvidos de Diferenciabilidade

Ver Teoria

Exercício 124 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100

Enunciado

USP, Sem Campus, Cálculo 1, Listas de Cálculo 1 - USP - Lista 1, Questão 7.8

Sejam derivável e tais que . Determine qual das

alternativas abaixo implica a existência de um c entre tal que

Passo 1

Fala galera, tudo bem com vocês? Vamos para mais uma questão de Cálculo 1.

Queremos Determinar a condição que implica a existência de um c entre tal que

Sabendo que

derivável e tais que .

Passo 2

Vamos começar pensando nas condições necessárias para podermos ter uma raiz entre duas.

Bem, para função que passou em um zero poder passar por por outros 2, ela precisa crescer e decrescer em seguida, a decrescer e crescer em seguida. Como na figura abaixo

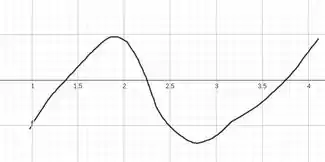
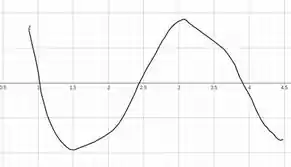
Ou seja, ao olharmos as derivadas, vemos que é preciso que

Prontinho pessoal!! Finalizamos mais uma questão. Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊

Resposta

Exercícios de Livros Relacionados

Faça o gráfico da função f x = x + x . Dê um zoom primeiro em direção ao ponto (-1,0) e então em direção a origem. Qual a diferença entre os comportamentos de f próximo a esses dois pontos? O que você

Lembre-se de que uma função f é chamada par se f - x = f ( x ) para todo x em seu domínio, e ímpar se f - x = - f ( x ) para cada um destes x . Demonstre cada uma das afirmativas a seguirA derivada de

Seja f : R → R uma função tal que quaisquer que sejam x e t f x - f t ≤ x - t 2 Calcule f ' x .

Suponha f definida em R , derivável em 0 e f 0 = 0 . Prove que existe g definida em R , contínua em 0 , tal que f x = xg x para todo x .

Sejam f e g definidas em R , com g contínua em 0 , e tais que, para todo x , f x = xg x . Mostre que f é derivável em 0 .