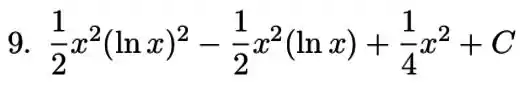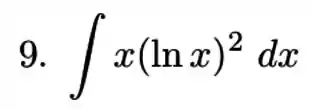
Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Integração por Partes

Ver Teoria
Exercício 137123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Passo 1

Integração por partes né? Do que a gente precisa? Determinar quem vai ser u   e   d v , certo? Vamos lembrar do nosso macete para escolher o u , o LIATE (logarítmica, inversa trigonométrica, algébrica, trigonométrica e exponencial).

Então nesse caso,

u = ln ⁡ x 2

d v = x   d x

Passo 2

Escolhidos u   e   v , precisamos encontrar d u   e   v

u = ln ⁡ x 2

Derivando

d u = 2 ln ⁡ x x d x

E

d v = x   d x

v = x 2 2

Vamos omitir as constantes aqui,beleza? Lá no final a gente coloca a constante geral.

Passo 3

Pronto! Com u , d u , v   e   d v determinados, agora vamos aplicar na regrinha da integração por partes que é:

∫ u   d v = u v - ∫ v   d u

Aplicando

∫ x   ln ⁡ x 2 d x = ln ⁡ x 2 x 2 2 - ∫ x 2 2 2 ln ⁡ x x d x

∫ x   ln ⁡ x 2 d x = ln ⁡ x 2 x 2 2 - ∫ x ln ⁡ x d x

Passo 4

Sim, chegamos em mais uma integral por partes, antes de continuar precisamos resolver

∫ x ln ⁡ x d x

Para isso

u = ln ⁡ x

d u = 1 x d x

E

d v = x   d x

v = x 2 2

Então aplicando na expressão da integral por partes

∫ x ln ⁡ x d x = ln ⁡ x x 2 2 - ∫ x 2 2 1 x d x

∫ x ln ⁡ x d x = ln ⁡ x x 2 2 - 1 2 ∫ x d x

∫ x ln ⁡ x d x = ln ⁡ x x 2 2 - x 2 4

Passo 5

Resolvida a integral, podemos voltar para a expressão final do passo 3

∫ x   ln ⁡ x 2 d x = ln ⁡ x 2 x 2 2 - ∫ x ln ⁡ x d x

∫ x ln ⁡ x d x = ln ⁡ x x 2 2 - x 2 4

Então

∫ x   ln ⁡ x 2 d x = ln ⁡ x 2 x 2 2 - ( ln ⁡ x x 2 2 - x 2 4 )  

∫ x   ln ⁡ x 2 d x = x 2 ln ⁡ x 2 2 - x 2 ln ⁡ x 2 + x 2 4 + C

Nunca esqueça a constante de integração!

Resposta

Exercícios de Livros Relacionados

Calcule a integral.int_()^() z^3 e^z d z
Calcule a integral.int_()^() (x e^(2 x))/((1 + 2 x)^2) d x
Use a tabela de integrais ao final do livro para calcular as integrais 20 - ∫ t g - 1 x x 2d x
Primeiro faça uma substituição e então use integração por partes para calcular a integral. ∫ t 3e - t 2d t
Calcule a integral.int_0^(pi) x^3 cos x d x