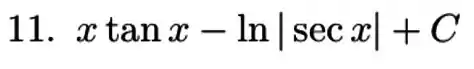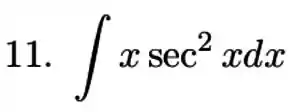
Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Integração por Partes

Ver Teoria
Exercício 101123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Passo 1

Vamos lá resolver essa integração por partes. Pra isso precisamos determinar quem vai ser u   e   d v . Vamos lembrar do nosso macete para escolher o u , o LIATE (logarítmica, inversa trigonométrica, algébrica, trigonométrica e exponencial).

No nosso caso então

u = x

d v = sec 2 ⁡ x

Passo 2

Beleza! Agora vamos encontrar d u   e   v

u = x

d u = d x

E

d v = sec 2 ⁡ x

v = tan ⁡ x

Passo 3

Para resolver então vamos substituir os passos anteriores na expressão de integração por partes

∫ u   d v = u v - ∫ v   d u

∫ x sec 2 ⁡ x d x = x tan ⁡ x - ∫ tan ⁡ x d x

Passo 4

Para resolver ∫ tan ⁡ x d x vamos usar a integração por substituição

∫ tan ⁡ x d x = ∫ sen ⁡ x cos ⁡ x d x

u 2 = cos ⁡ x

d u 2 = - sen ⁡ x d x

∫ tan ⁡ x d x = - ∫ d u 2 u 2

∫ tan ⁡ x d x = - ln ⁡ u 2

Substituindo novamente

∫ tan ⁡ x d x = - ln ⁡ cos ⁡ x

Podemos reescrever isso como

- ln ⁡ cos ⁡ x = ln ⁡ cos ⁡ x - 1 = ln ⁡ sec ⁡ x

Passo 5

Resolvida a integral vamos substituir o que encontramos lá na nossa expressão do passo 3.

∫ x sec 2 ⁡ x d x = x tan ⁡ x - ∫ tan ⁡ x d x

∫ x sec 2 ⁡ x d x = x tan ⁡ x - ln ⁡ sec ⁡ x + C

Não se esqueça de adicionar a constante no final!

Resposta

Exercícios de Livros Relacionados

Calcule a integral.int_()^() z^3 e^z d z
Calcule a integral.int_()^() (x e^(2 x))/((1 + 2 x)^2) d x
Use a tabela de integrais ao final do livro para calcular as integrais 20 - ∫ t g - 1 x x 2d x
Primeiro faça uma substituição e então use integração por partes para calcular a integral. ∫ t 3e - t 2d t
Calcule a integral.int_0^(pi) x^3 cos x d x