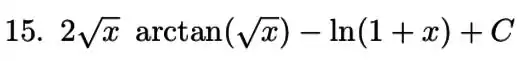![]()
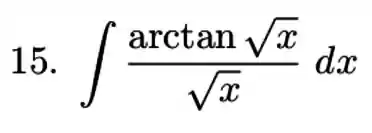
Passo 1
Integração por partes né? Do que a gente precisa? Determinar quem vai ser , certo? Vamos lembrar do nosso macete para escolher o , o LIATE (logarítmica, inversa trigonométrica, algébrica, trigonométrica e exponencial).
No nosso caso temos uma inversa trigonométrica, então
Passo 2
Escolhidos , precisamos encontrar
Derivando
Essa é uma daquelas derivadas mais chatinhas de fazer, se ficar com dúvida volta lá nos tópicos de derivação que tá mais detalhado. Vamos continuar
Vamos omitir as constantes aqui,beleza? Lá no final a gente coloca a constante geral.
Passo 3
Pronto! Com determinados, agora vamos aplicar na regrinha da integração por partes que é:
Aplicando
Resolvendo a integral
Prontinho! Não esquece da constante viu?
Resposta