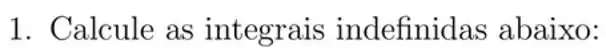
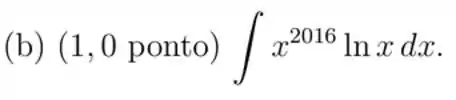
Passo 1
Vamos usar a integração por partes nesse cara aí! Pelo LIATE, vamos ter o seguinte:
Passo 2
Assim, teremos o seguinte, pela fórmula da integral por partes:
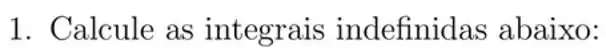
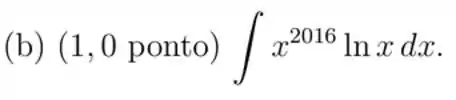
Vamos usar a integração por partes nesse cara aí! Pelo LIATE, vamos ter o seguinte:
Assim, teremos o seguinte, pela fórmula da integral por partes: