UFSC – Cálculo 1 – Lista 4.6 – Questão 2b
Calcule as integrais indefinidas abaixo
Passo 1
Oi, tudo bem? Essa integral parece complicada de resolver, mas vou te ajudar! Precisamos resolver essa integral aqui:
Logo de cara vemos que tem uma exponencial de um polinômio de , o que deixa ele bem estranho. Não temos a derivada daquele no integrando, então não podemos usar a técnica da substituição simples. O que nos resta? POR PARTES!
Mas calma! Nota que no integrando temos o produto de duas funções:
Sendo que uma delas é fácil de integrar e a outra de derivar
Mas se não for obvio para você, pode também usar o LIATE para escolher quem será nosso , e por consequência, nosso :
Sendo assim vamos escolher e e aplicar a integração por partes! Essa é a ideia para resolver essa questão!
Mas calma, vou fazer passo a passo com você!
Passo 2
Precisamos integrar essa coisa:
Pelo nosso querido LIATE sabemos que a escolha de é , então nosso :
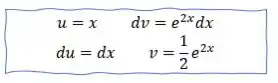
Tranquilo até aqui?
Agora precisamos colocar na integração por partes:
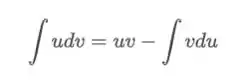
Fazendo as substituições temos:
Beleza? Vamos guardar esse resultado!
Passo 3
Estamos quase lá! Agora nossa missão é resolver aquela integral que surgiu na direita:
Não vai esquecer de colocar aquele no final, pois temos uma integral indefinida!
Agora sim! Terminamos!
Espero ter ajudado! Vamos para a próxima?