1) Calcule a integral
Onde .
Passo 1
Falaaa aí... Beleza???
Nessa questão vamos calcular a integral dupla:
E foi dada essa região , que vamos usar pra achar os limites de integração.
Lembrando que é pra simbolizar “área”, e que a área, no plano cartesiano, pode ser representada por , então podemos escrever:
Daí vamos ter:
Pra resolver uma integral dupla, primeiros integramos em relação a ou e o outro consideramos constante. Por exemplo, se formos integrar em relação a primeiro, vamos considerar o constante e podemos reescrever:
Depois integramos, o resultado dessa integral em , em relação a .
Vambora botar a mão na massa que tudo fica mais palpável.
Passo 2
Vamos começar esboçando a região pra achar os intervalos de integração:
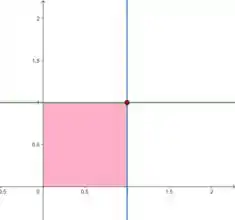
Oh... temos um quadrado bonitinho. E notamos que varia de 0 a 1 e também varia de 0 a 1. Esses são os limites de integração.
Show...
Passo 3
Agora precisamos decidir se vamos integrar primeiro em relação a ou em relação a .
Bom... como temos uma região retangular, então não vai fazer muita diferença. Podemos integrar em relação a ou a primeiro.
Escolhendo (e deixando constante), podemos reescrever:
Usando substituição simples, vamos resolver a integral de dentro :
Chamando de , ficamos com:
E para os intervalos de integração:
- em :
- em
Daí ficamos com:
Resolvendo a integral:
E, assim, a integral dupla vira:
Passo 4
“Só” falta calcular essa integral que sobrou. Vamos usar integração por partes (ninguém merece integrar ln, né? rs)
Lembrando que a integração por partes é algo do tipo:
Podemos escrever:
Vamos chamar, de forma que o ln suma (derivando o bichinho, né?):
Daí ficamos com:
Passo 5
Resolvendo a última integral , vamos usar substituição simples, de novo:
Chamando de . Agora temos uma peculiaridade. Vamos fazer uma manipulação pra fazer a mágica acontecer:
Então:
Resolvendo:
Voltando pra :
Temos:
Substituindo pra achar o resultado:
Então:
Ufaa... essa foi pesadinha, heim!? Mas acabamos \o/
Bora pra próxima?