P3 – Cálculo Diferencial e Integral 2 – 2021.2 – Profª Cláudia Brunosi Medeiros
Calcule , onde é a região limitada pelas retas , e .
Passo 1
Vamos entender melhor essa região D para podermos reescrever aquele termo e transformar numa integral que a gente consiga resolver. Desenhando as três funções do enunciado temos
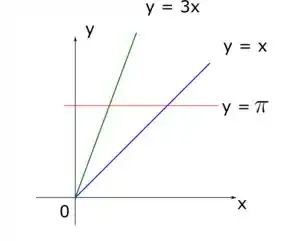
Olha só! Naquele miolo ali surge um triangulo que é a nossa região de integração
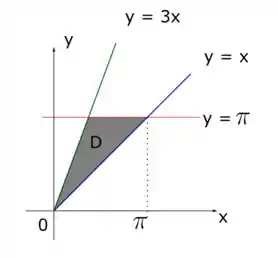
A gente percebe que as funções se encontram na origem no nosso sistema () e o ponto mais à direita desse triângulo é o encontro de com . Ou seja, igualando essas duas funções temos
Que é o maior valor de x que podemos. Olhando essa figura a gente percebe que a região é uma região do tipo 1 com os limites
Passo 2
Como em uma região do tipo 1 temos
A gente usa essa informação e os limites que a gente já encontrou para reescrever a integral como
Essa integral iterada pode ser resolvida primeiro resolvendo a integral em isoladamente
Passo 3
Agora a gente resolve a integral em que sobrou
Vamos ter que usar o método de integral por partes escolhendo e . Calculamos pela derivada
E obtemos integrando
Usando
A gente escreve a nossa integral como
Passo 4
Essa é uma integral iterada e a gente pode resolvê-la primeiro resolvendo a integral em separadamente
Passo 5
Agora podemos resolver a integral em