Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Integração por Partes

Ver Teoria
Exercício 207123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

UFSCAR – Cálculo 1 – P3 – Questão 2c

Calcule as seguintes integrais

c )   ∫ 1 3 1 + x 2 x 2 d x

Passo 1

Oi pessoal, tudo bem? O problema nos deu essa integral aqui para resolver

∫ 1 3 1 + x 2 x 2 d x

A pergunta de milhões: qual técnica de integração usar?

Você percebe que ali dentro tem duas funções que não são nem derivada uma da outra e nem uma forma tabelada??

Então a ideia aqui é o seguinte: usar a técnica de integração por partes

Mas relaxa, vou fazer com você!

Passo 2

Precisamos resolver essa integral

∫ 1 3 1 + x 2 x 2 d x

Já conversamos sobre usar o método de integração pos partes, então bora lá:

u = x 2 + 1 → d u = x x 2 + 1 d x

d v = 1 x 2 d x → v = - 1 x

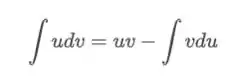Lembrando que por partes é assim

Agora vamos substituir:

∫ 1 3 1 + x 2 x 2 d x = - 1 + x 2 x 1 3 + ∫ 1 3 - 1 x x x 2 + 1 d x

= - 1 + x 2 x 1 3 + ∫ 1 3 1 x 2 + 1 d x

Tudo bem até aqui?

Passo 3

Essa segunda integral vou resolver em separado:

∫ 1 3 1 x 2 + 1 d x

Como temos algo do tipo x 2 + a 2 , vamos usar substituição trigonométrica!

x = t g θ

d x = sec 2 ⁡ θ d θ

Substituindo temos

∫ sec 2 ⁡ θ d θ t g 2 θ + 1 = ∫ s e c θ d θ = ln ⁡ ( s e c θ + t g θ )

x = t g θ , então podemos formar o seguinte triângulo retângulo

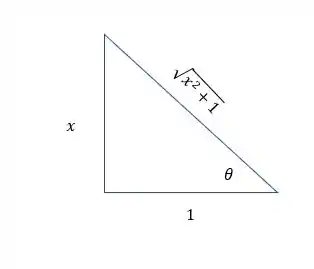
Assim temos que

t g θ = x

s e c θ = x 2 + 1

Agora sim nossa integral está resolvida

∫ s e c θ d θ = ln ⁡ ( s e c θ + t g θ ) = ln ⁡ x 2 + 1 + x

Beleza? Vamos retornar para a integral do problema?

calma, estamos quase no fim!

Passo 4

Do passo dois tínhamos essa integral aqui

∫ 1 3 1 + x 2 x 2 d x = - 1 + x 2 x 1 3 + ∫ 1 3 1 x 2 + 1 d x

E resolvemos aquela integral da direita no passo 3:

∫ 1 3 1 + x 2 x 2 d x = - 1 + x 2 x 1 3 + ln ⁡ x 2 + 1 + x 1 3

Agora nos resta aplicar nos limites de integração!

∫ 1 3 1 + x 2 x 2 d x = - 2 3 + ln ⁡ 2 + 3 + 2 - ln ⁡ 2 + 1

Agrupando os termos temos nosso resultado final

∫ 1 3 1 + x 2 x 2 d x = 6 - 2 3 + ln ⁡ 2 + 3 1 + 2

Agora sim! Terminamos!

Espero ter ajudado!

=D

Resposta

6 - 2 3 + ln ⁡ 2 + 3 1 + 2

Exercícios de Livros Relacionados

Calcule a integral.int_()^() z^3 e^z d z
Calcule a integral.int_()^() (x e^(2 x))/((1 + 2 x)^2) d x
Use a tabela de integrais ao final do livro para calcular as integrais 20 - ∫ t g - 1 x x 2d x
Primeiro faça uma substituição e então use integração por partes para calcular a integral. ∫ t 3e - t 2d t
Calcule a integral.int_0^(pi) x^3 cos x d x