Explique que procedimento usar para calcular a integral (não precisa calcular, apenas o caminho)
Passo 1
E aí pessoal, tudo bem?
Essa questão parece complicada, mas vou ajudar você aqui! Já sabemos que funções que não estão divididas entre função e derivada no integrando, devem ser integradas pela técnica da integração por partes, certo?


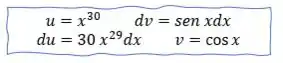
E aplicando a fórmula da integração temos:
Teremos uma integral à direita, certo? Mas para resolver essa integral vamos precisar aplicar novamente a técnica de integração por partes!

Passo 2
Mas, será que isso terá um fim?

Terá sim! Fazendo a escolha de sempre sendo o polinômio, a integral que aparecerá à direita terá sempre um grau a menos, pois vamos derivar !
Assim vamos repetindo o processo da integração por partes até que haja uma integral apenas na função trigonométrica, ocasionando em um resultado sem integrais.

Ainda mais que a função seno é periódica, e sua derivada é outra função trigonométrica, que por sua ver tem derivada trigonométrica...
E isso também irá se repetir se tivermos o produto de um polinômio por uma exponencial! Lembra que a derivada da exponencial é ela mesma! Então a ideia é sempre escolher o polinômio como , e ir derivando, até que o grau seja (ou seja, constante) e finalmente a integração acabe!

E é isso!
Espero ter ajudado! Vamos para a próxima?
Resposta
explicação