UNB – Sem Campus – Cálculo 1 – Listas – Listas de Aplicações Calculo 1 – UNB – Questão 2
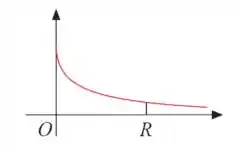
A figura ao lado ilustra o gráfico da função , . A área sob esse gráfico entre e é dada pela integral
Use uma mudança de variáveis para transformar a integral indefinida em uma outra cujo integrando não envolva a função raiz quadrada.
Calcule a integral do item anterior usando integração por partes.
Usando os resultados anteriores, determine explicitamente a função .
Calcule o limite usando a regra de L’Hospital, e verifique se a área sob o gráfico da , para , é finita.
Passo 1
Oiie, tudo certinho contigo?
O enunciado nos dá uma função definida em um intervalo, e pede para calcularmos a área em função de uma constante qualquer pertencente ao intervalo dado. Para a primeira alternativa será suficiente fazer uma substituição simples, o que nos levará a uma integral por partes como pede a a segunda alternativa. A alternativa é aplicar os limites de integração dados no enunciado na integral resolvida na alternativa anterior, e por último, iremos avaliar o limite quando em nosso resultado!
Vamos com calma em cada uma delas! Boa sorte para nós! E Bora lá!
Passo 2
A primeira coisa é tentar reescrever a integral! Temos o seguinte
Se usarmos que
Usando novamente que , temos que . Nossa integral se torna então
A alternativa já foi! Agora vamos resolver essa integral para a alternativa .
Passo 3
O enunciado sugere utilizar integração por partes, e é uma boa ideia, lembrando de utilizar LIPTE (Logaritmo, Inversa, Polinomial, Trigonométrica, Exponencial) para estabelecer qual função você deve dar preferência na hora de escolher o seu e na expressão
Neste caso, temos que e . Ou seja, a integral toma a forma
A nova integral que ainda está em aberto pode ser identificada como
De forma que
Ou seja, temos que
Vamos para a alternativa agora!
Passo 4
Ele pede para que resolvamos a seguinte integral
Nós já resolvemos a integral no passo anterior, então temos que aplicar os limites de integração! Da seguinte maneira
Se lembrarmos que , podemos escrever que e . Portanto, precisamos resolver o seguinte
Ou, resumidamente, temos
Tendo esta expressão em mão! Falta só calcular o limite pedido na alternativa . Vamos lá!
Passo 5
Para acabar! Vamos calcular então
Note que ao tender , temos uma indeterminação do tipo no segundo termo. Portanto, podemos aplicar o método de L’Hospital e derivar tanto o numerador quando o numerador e reaplicar o limite! Vem comigo!
Passo 6
Temos o seguinte
E, também que
Voltando em nosso limite, temos
Quando , temos que o segundo termo agora vai a , portanto, temos que
A questão foi isso! Te vejo na próxima! Tchauzinho!
Resposta