5. Considere a função dada por e as seguintes afirmações
- é injetora
- é sobrejetora
- é inversível e sua inversa é dada por
- O gráfico de intercepta o eixo em apenas um valor
Quantas afirmações são verdadeiras:
Passo 1
Oi, galerinha! Tudo bom? Aqui nós temos que verificar qual frase é verdade, com base na função dada. Repare que as afirmações são sobre funções sobrejetoras e injetoras. Então vamos revisar essas definições!
Para quem não lembra:
- Uma função é injetora se para dois pontos quaisquer pertencentes ao domínio de :
Tivermos:
- Uma função é sobrejetora se para cada valor de existir ao menos um valor de associado:
Agora bora analisar por partes!
Passo 2
Vamos começar avaliando se ela é injetora e sobrejetora. Repara que temos, uma divisão de função do primeiro grau! E toda função do primeiro grau é injetora e sobrejetora. Então a nossa função também será injetora e sobrejetora.
O gráfico ficaria mais ou menos assim:
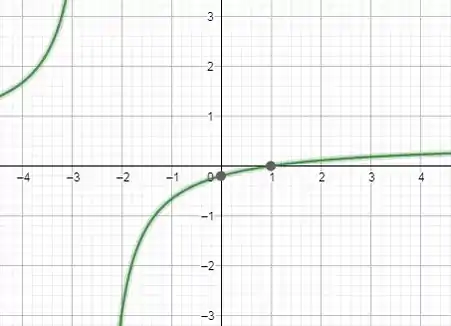
Logo, a e são verdadeiras.
Passo 3
Agora vamos avaliar a sua função inversa! Temos que
Transformando tudo que é em e vice-versa, ficamos com
Ao isolar , teremos a nossa função inversa . Ela ficará assim,
Colocando em evidencia,
Multiplicando por
Logo,
Logo a afirmação é verdadeira.
Passo 4
Por fim, temos a seguinte afirmação: gráfico de intercepta o eixo em apenas um valor. Como vimos no Passo 2, o gráfico só corta o eixo em . Logo todas alternativas são verdadeiras.