UTFPR - Cálculo 1 - Provas - P1 - 2019.1 - questão 7
Seja . Responda
- Determine o domínio da função.
- Calcule .
- Calcule o valor de para que a função abaixo seja contínua em
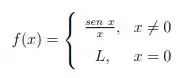
Passo 1
Olá pessoal lindo do Responde Aí, tudo bem? Essa questão parece complicada, mas vou ajudar você aqui! Vamos começar?
Bom a nossa questão traz uma função . Tudo tranquilo né?
Já na letra a é pedido ao aluno que se encontre o domínio da função. Vocês lembram o que é o domínio de uma função???
O domínio de uma função nada mais é que o conjunto de todas as entradas possíveis da função, ou seja, são todos os valores em que pode assumir.
Olhando para a nossa função :
→ Temos que deve ser diferente de , uma vez que aparece no denominador da nossa função e sabemos que não existe divisão por né?
→ Já olhando para o numerador temos uma função trigonométrica , como se trata de uma função trigonométrica temos que o domínio é o conjunto dos números reais(.
Assim, para atender ambos os critérios afirma-se que o domínio da função será
Passo 2
Agora meu povo, vamos para a letra b.Na letra b é pedido que se calcule o . Então temos que descobrir o valor do limite de quando o tende a . E aí? como faremos essa letra???
Tenho uma super dica para vocês, possivelmente o professor pode já ter comentado sobre esse limite fundamental ou você pode ter visto em algum outro lugar, devido ao fato de esse limite ser bastante requisitado. Então bora lá!
Gravem esse limite em suas mentes será muito importante!!!
Passo 3
A letra c quer que você seja capaz de determinar o valor de para que a função seja contínua em , sendo que :
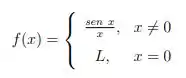
Meu Deussss e agora??? Deve tá se passando pela sua cabeça o famoso pensamento “Humm e se eu trancar o curso??” hahaha
Calmô, bora fazer juntinhos! Uma função é contínua num ponto de seu domínio quando . Quando é contínua em cada ponto de seu domínio, dizemos que é contínua. Logo,
Como na letra anterior já descobrimos quanto é o valor desse limite :
Dessa forma, podemos afirmar que deve ser igual a , ou seja, será uma função constante para .
Lembrando que , sendo uma constante.
E aí??? Essa resolução te ajudou? Responde Aí!
Bons Estudos, Galera!!!
Resposta
a)
b)
c)