Dê um exemplo (que pode ser gráfico) de uma função definida em tal que , mas não possui raiz em . O que se pode afirmar sobre a continuidade desta função?

Temos uma função qualquer, vou desenhar de azul, ok? E sabemos que em um ponto essa função tem uma imagem negativa (abaixo do eixo ). Em outro ponto ela tem uma imagem positiva (acima do eixo ), tudo isso dentro do intervalo . Só que temos um porém: a função não tem raiz nesse intervalo! Ela não corta o eixo ! Então essa situação pode ser representada assim

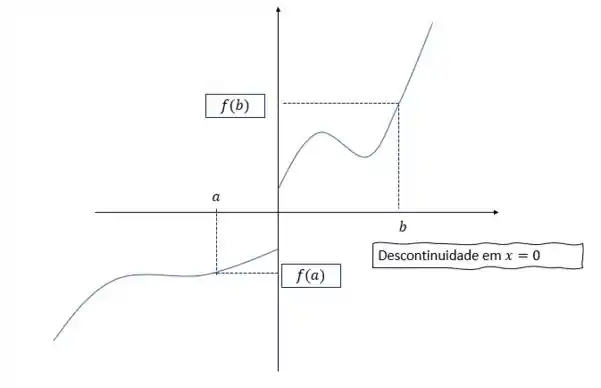
Viu que em ela deu um salto? Quando temos esse salto no gráfico de uma função, precisamos tirar o lápis do papel para poder resolver ela não é mesmo?

Isso significa que nesse ponto a função apresenta uma descontinuidade!

E vemos que isso claramente acontece com a função !

Portanto concluímos que a função não é contínua!

E é isso! Espero ter ajudado!