UFRJ, Sem Campus, Cálculo 1, Listas de C1 - Profº Jair - Primeira Edição V1.3, Questão 0.5c
Estude o sinal (determine onde é positiva e onde é negativa) das funções
Passo 1
Faaaala galera, tudo beleza?
Nessa questão recebemos a função:
E, precisamos determinar quais os intervalos em que é positiva ou negativa.
Para isso, é importante a gente perceber que a função trata-se de uma equação do grau, ou seja, seu gráfico é de uma parábola.
Como o termo que multiplica é positivo, a função deve ser negativa entre as raízes, nula nas raízes, e positiva no intervalo restante.
Se a função não tiver raízes, ou tiver uma raiz dupla, precisaremos olhar pro valor justamente desse termo que multiplica pra determinar a solução.
Então vamos lá, colocar a mão na massa! 😊
Passo 2
Bom, pra começar vamos calcular as raízes da equação do segundo grau que representa .
Essa equação representa o produto notável do quadrado da soma, lembram?
Nesse caso, temos .
Logo, podemos fatorar a expressão como sendo:
Agora é tranquilo analisarmos as raízes dessa equação. Para zerar a equação acima, basta a gente fazer:
Além disso, esse é o único valor que zera a expressão:
Por isso, concluímos que:
É uma raiz dupla!
Sendo assim, precisamos olhar para o termo que multiplica , ou seja, o coeficiente .
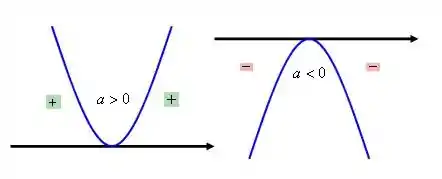
Como na nossa equação , temos que é sempre positivo, exceto em , onde a função é nula.
E aí galera, pegaram a ideia?
Obrigado pela atenção e até a próxima 😊