Represente por diagrama de flechas e verifique se são funções de cada relação abaixo:
a) , sendo
b) sendo
Passo 1
Show o que a gente precisa observar é que para ser uma função TODO elemento do Domínio (Conjunto A nesse caso) precisa se relacionar a UM ÚNICO elemento do CONTRADOMÍNIO (Conjunto B nesse caso).
Então, o que vamos fazer é colocar os elementos de A na nossa lei de formação e ver o que acontece.
Por exemplo,
Para teremos
Para teremos
Para teremos
E assim por diante...
Depois é só a gente relacionar os valores de um conjunto com o do outro e encontraremos algo assim:
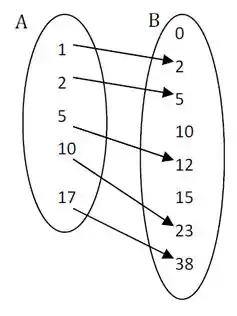
Agora vamos observar duas coisas:
- Se todo elemento do domínio está se relacionando com alguém
- Se os elementos do domínio estão relacionados a um único elemento do contradomínio
Essas duas condições estão sendo satisfeitas, logo é uma função de A em B =D
Passo 2
Vamos repetir o processo para a letra b)
Temos agora a seguinte lei de formação:
Esses são os valores que x pode assumir:
Para teremos
Para teremos
Para teremos
E assim por diante...
Montando os dois conjuntos e os relacionando, teremos:
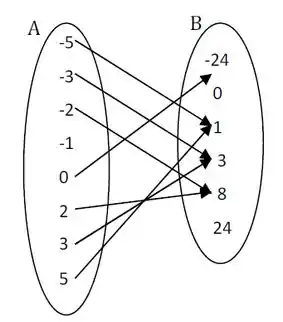
Opa, espera um pouco, percebeu que o não está relacionado com ninguém? Observa só:
Para teremos
Se tivermos temos uma indeterminação.
Logo, não vai atingir nenhum elemento de B, sendo assim NÃO será uma função. Pois nem todo elemento do Domínio está relacionado a um elemento do contradomínio.
Resposta
- É uma função.
- Não é função.