USP, Sem Campus, Cálculo 1, Listas de Cálculo 1 - USP - Lista 1, Questão 7.15
. Para quais valores de a equação tem exatamente duas
soluções reais?
Passo 1
Fala galera, tudo bem com vocês? Vamos para mais uma questão de Cálculo 1.
Queremos Determinar para quais valores a equação tem soluções reais, onde
Bem, vamos resolver!!!
Passo 2
Para termos duas soluções reais, para a equação abaixo
precisamos cruzar o eixo duas vezes, ou seja, precisamos ter variações no sinal da derivada. Vamos fazer o estudo de sinal da derivada de
Derivando
Note que o sinal da derivada é determinado exclusivamente por
Logo, temos que a função é decrescente de
e crescente no restante.
Dessa forma, podemos fazer o seguinte esboço da nossa função
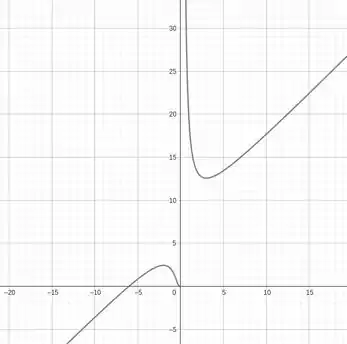
Passo 3
Ou seja, para termos duas soluções, para
podemos transladar o gráfico para baixo até antes do ponto onde uma das derivadas é zero. Que como vimos no passo anterior. São os pontos
Logo, como o valor da função em é temos que
Agora, também podemos ter mais soluções ao descermos o gráfico a ponto de tocar o ponto onde a segunda derivada é zero, que ocorre quando . E como o valor da função nesse ponto é
Temos que
Prontinho pessoal!! Finalizamos mais uma questão. Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊
Resposta
Desenvolvimento acima