Determine o domínio maximal das seguintes funções , em que
Passo 1
O domínio maximal é o maior domínio que podemos pegar para função.
Para encontra-lo, temos que olhar os casos onde a função não existiria.
São 3:
- Denominador
- Radicando
- Logaritmando
Lembrando que o radicando é a expressão dentro da raiz de par, e o logaritmando é o valor dentro do Log.
Passo 2
Aqui, temos uma raiz quadrada, então o valor dentro dela, o radicando, precisa ser maior ou igual a zero
Temos que abrir os dois módulos
primeiro vamos pegar
Resolvendo aquela inequação, vamos ter
E
Mas como é natural, ele só vai existir no primeiro intervalo, então
O outro módulo não precisamos nem abrir, isso porque é sempre positivo.
A nossa inequação vai ficar
Passo 3
isso é uma função de segundo grau, vamos resolver como se fossem nos reais e depois vemos quais naturais estão no itnervalo
Vamos começar achando suas raízes
AS raízes vão ser
E
Como , o seu gráfico será algo assim
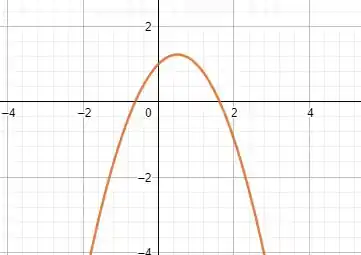
Entre as raízes é negativo e fora é positivo.
Como ele quer a parte positiva, vamos pegar
Passo 4
Vamos tentar ver quais naturais estão ali.
Primeiro, podemos ver que
Então
O primeiro natural será o
Vamos olhar a outra parte do intervalo, como isso vai ser limitado, basta testarmos os próximos naturais até não funcionar mais
Opa, esse já falhou
Os naturais vão ser só o e o .