UFRJ, Sem Campus, Cálculo 1, Listas de C1 - Profº Jair - Primeira Edição V1.3, Questão 0.5d
Estude o sinal (determine onde é positiva e onde é negativa) das funções
Passo 1
E aí gente bonita do RA, como vocês estão?
Nessa questão recebemos a função:
E, precisamos determinar quais os intervalos em que é positiva ou negativa.
Para ser positiva precisamos que o numerador e o denominador tenham o mesmo sinal. Se tiverem sinais contrários, a função será negativa.
Além disso, como trata-se de uma fração, o denominador não pode ser nulo.
Portanto, pra fazer o estudo de sinal dessa função, vamos fazer o estudo de sinal separadamente do numerador e do denominador, e depois consideramos os casos. Beleza?
Vamo nessa!
Passo 2
Começando pelo numerador, temos:
Logo:
Na igualdade, o numerador é nulo. E, entre os dois valores, o numerador é negativo.
Ou seja:
Excelente!
Podemos resumir através da seguinte imagem:
Passo 3
Já para o denominador, vamos ter:
Tirando a raiz, vamos ter:
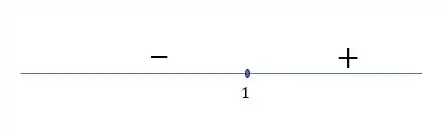
Logo:
Excelente!
Podemos resumir através da seguinte imagem:
Passo 4
Agora devemos juntar os dois resultados, analisando o intervalo de valores em que o numerador e denominador terão o mesmo sinal.
Podemos usar as imagens que mostramos antes para facilitar esse processo:
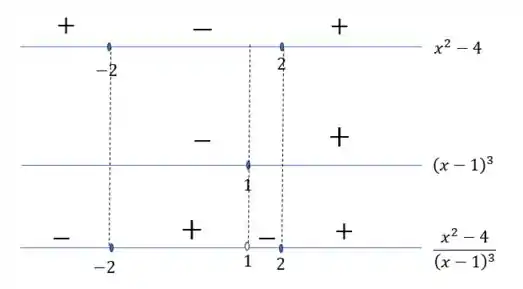
O que fizemos foi basicamente superpor os sinais em cada um dos intervalos. Considerando que numa divisão, dividir números positivos, ou dividir números negativos, resulta em um número positivo. E, dividir número positivo com negativo, resulta em um número negativo.
Em temos uma bola aberta, pois esse ponto zera o denominador. Logo, ele não pertence ao domínio de .
E aí pessoal, sacaram a ideia?
Muito obrigado pela atenção 😊
Resposta
Resposta no texto.