UFRJ, Sem Campus, Cálculo 1, Listas de C1 - Profº Jair - Primeira Edição V1.3, Questão 0.3g
Dada a função , determine:
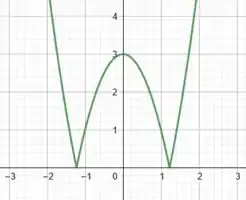
g) um esboço do gráfico de
Passo 1
Fala aí pessoal, tudo bem?
Nessa questão recebemos uma função de dada por:
Precisamos esboçar o gráfico da função:
Ou seja, temos que esboçar o gráfico do módulo de . Vocês lembram o que o módulo faz com o gráfico de uma função?
Basicamente, ele reflete, com relação ao eixo , toda a parte gráfica que estiver abaixo desse eixo. Sendo assim, vamos primeiro esboçar o gráfico de e depois calculamos o módulo através desse rebatimento.
Vem com a gente que vai ficar bem claro 😊
Passo 2
Bom, vamos começar pensando no gráfico de .
Temos que:
Ou seja, é uma equação do segundo grau, logo trata-se de uma parábola.
Para esboçar o seu gráfico vamos determinar as suas raízes e o ponto de vértice dessa parábola:
Logo:
Essas são as raízes de .
Para calcular o vértice da parábola, podemos usar que:
Onde é o coeficiente que multiplica , e o coeficiente que multiplica .
Assim, no nosso caso teremos:
Logo, a nossa parábola está virada para cima (pois ), possui raízes , e possui do vértice igual a zero.
Assim, temos:
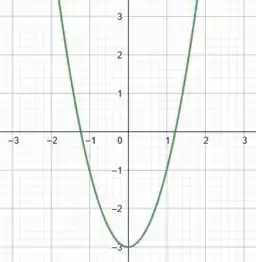
Muito bom!
Passo 3
Agora vamos aplicar o módulo nesse gráfico que encontramos.
Para isso, basta refletirmos o pedaço do gráfico entre as duas raízes, pois esse pedaço é negativo.
Daí, vamos ter:
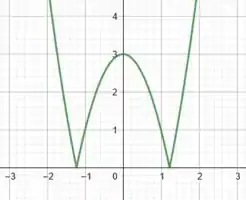
Prontinho!
Curtiram a solução? Responde Aí!
Resposta
