UFSC – Pré-Cálculo – Exame de Proeficiência – 2018.1 – Questão 8
Seja e funções definidas por
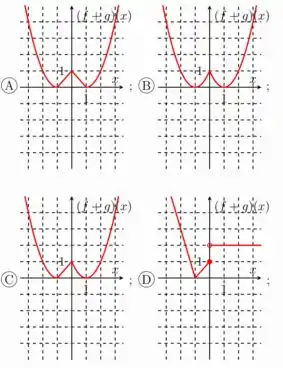
O item que melhor representa o gráfico de é
Passo 1
Faaala pessoal, tudo tranquilo?
Se liga só, temos essas duas funções:
Que são funções definidas em partes, ou seja: dependendo do valor de , elas podem ter comportamentos diferentes
E aí queremos definir qual gráfico representa a função , que é a soma dessas duas funções
Caaalma, vai dar tudo certo!
O primeiro passo nesse exercício é definirmos os intervalos onde a função vai variar. Isso vai acontecer em cada “quebra” tanto de quanto de :
Show! Então é nesses intervalos que vamos analisar a soma das funções, bora!
Passo 2
Para , vamos ter
Ou seja, o é uma reta e é uma parábola
A soma das funções vai ser
Que é uma parábola também hehehe
Ou seja, para , a soma das funções vai ser uma parábola. Então já podemos descartar a alternativa D 😉
Passo 3
Para , temos
Então a soma das funções vai ser
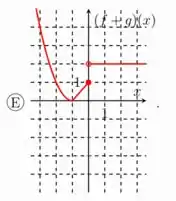
Então, entre e vamos ter uma reta crescente.
Já podemos descartar a opção B, que nos mostra uma parábola nesse intervalo hahaha
Passo 4
Por fim, para , temos
Então a soma das funções vai ser
Opa, então nesse intervalo a soma das funções é uma reta constante, que vale sempre 2
O único gráfico que condiz com as funções que encontramos para cada intervalo é o da letra E :P