UnB – Cálculo 1 – Lista de Exercícios 3 – Questão 14
Sejam e funções contínuas em , tais que e . Mostre que a equação tem solução.
Passo 1
Fala galera, tudo bem? Essa questão parece complicada, mas estou aqui para te ajudar! Vamos resolver juntos?
O problema nos disse que temos duas funções e e que ambas são contínuas em um determinado intervalo fechado
Tudo bem até aqui?
E o problema também nos disse como essas funções se comportam nos extremos desse intervalo. No início dele, em
Ou seja, a função está acima da função
E no outro extremo, em
Dito isso, o problema pede para mostrar que a equação
Tem solução. Mas como fazer isso? A ideia aqui é colocar essas informações em um gráfico genérico e observar se essa igualdade acontece!
Mas relaxa, vou fazer passo a passo com você!
Vamos começar?
Passo 2
Temos duas funções quaisquer, vou desenhar de azul e de vermelho, ok? E sabemos que essas funções são contínuas dentro do intervalo . Sabemos também que a começa por cima, mas que em algum momento, ela termina embaixo da . Essa situação pode ser representada assim
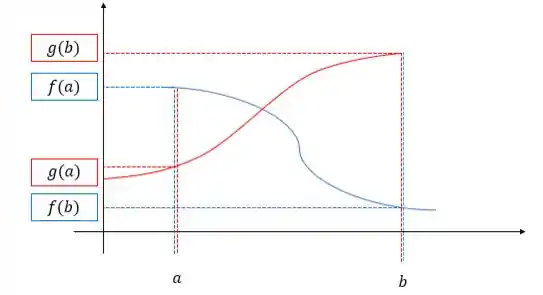
E o problema pede para que mostremos que a equação
Tem solução. Ora ora, o que significa graficamente a função ser igual a função ?
Significa que elas se cruzam!
E vemos que isso claramente acontece com as funções e !
Como as funções são contínuas, temos certeza de que não é preciso ‘tirar o lápis do papel’ para esboçar as duas, então como a começa embaixo da e termina em cima, isso significa que em algum momento as duas valem o mesmo!
Tendo assim solução!
E é isso! Espero ter ajudado!