UFSC – Pré-Cálculo – Exame de Proeficiência – 2018.1 – Questão 8
Seja definida por . A inversa de é a função dada por
a)
b)
c)
d)
e)
Passo 1
E aíí gente, tudo belezinha?
Se liga, temos uma função que o domínio vai de até :
Então temos só uma parte de uma parábola, que é a parte que vem lááá da esquerdona até chegar em . Depois disso não tem mais nada! Em , temos
Que é exatamente onde começa a imagem da função. Então temos algo nesse estilo:
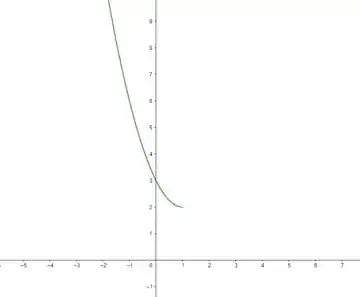
E aí queremos encontrar a função inversa de , lembrando que o domínio vira a imagem e a imagem vira o domínio hahahaha
Para isso, vamos fazer , trocar e de lugar e aí isolar o . Bora?
Passo 2
Temos
Trocando por :
(se liga no bizu: sempre que formos inverter uma função quadrática, o esquema depois dessa troca é resolver a equação para . Isso vai nos dar duas soluções, mas temos que focar naquela solução que ta no contra-domínio que foi dado pelo enunciado, beleza?)
Então vamos resolver isso para :
Então:
Dividindo em cima e embaixo por :
Então, nossas soluções são
Beleza, agora vamos ver qual dessas soluções satisfaz o contra-domínio do enunciado
Passo 3
Queremos que o contra-domínio venha lááá de até chegar em , no eixo vertical.
Vamos analisar nossas soluções:
Para , conforme o valor de vai crescendo de até , o valor de também cresce. Se for por exemplo, o também vai ser um número muito grande, vai indo lá pra
Por outro lado, em , se o for crescendo muito (de até ), o vai diminuindo, porque temos menos alguma coisa muito grande. Isso vai dar um número negativo absurdo HAHAHAHA
Então, quando vai crescendo no nosso domínio, o vai diminuindo mais e mais, indo lá pra
Portanto, quem obedece o requisito de que em algum momento o contra-domínio vai ser negativo é o :
Essa é a nossa função inversa com o domínio e contra-domínio dados
Então a alternativa correta é a letra C