Determine a equação do plano tangente à superfície , com e maiores do que , que forma um tetraedro mínimo com os planos coordenados.
Passo 1
Vamos organizar nossa linha de pensamento, porque, honestamente, é bem fácil se perder nesse enunciado... O principais pontos são:
- Temos uma superfície ,
- que tem um plano tangente num ponto , de equação .
- Além disso, esse plano tangente forma um tetraedro de volume com os planos coordenados.
- Qual é a equação do plano tangente que forma um tetraedro de volume mínimo?
Sério, quando li isso pela primeira vez foi tipo “Sabendo que os golfinhos se reproduzem em outubro, calcule a massa da Terra”. Mas vamos ver o que podemos tirar desse enunciado XD
A jogada aqui é pensar o seguinte: Com a equação da superfície, podemos descobrir uma equação para o plano num ponto genérico . Com essa equação genérica para o plano, podemos encontrar um volume genérico para o tetraedro. Então, vamos minimizar a função do volume, que vai ter como restrição o conjunto de todos os pontos possíveis de tangência para o plano tangente, ou seja, a própria equação da superfície .
Passo 2
Primeiramente, temos que encontrar uma equação para o volume do tetraedro. Dá uma olhada no plano :
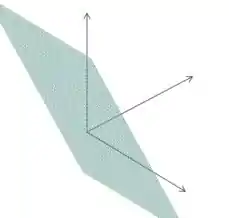
Se der uma girada nos eixos dá pra ver certinho que é uma pirâmide de base triangular:
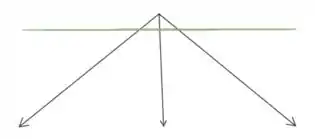
Pela primeira pode não dar pra ver direito (desculpa), mas pela equação do plano, vemos que ele corta os eixos coordenados nos pontos , e .
Se fosse um plano genérico , ele cortaria o eixo em (para saber isso basta anular as variáveis e na equação do plano). De maneira análoga, cortaria o eixo em e em .
Aí vai um conteúdo de Ensino Médio: Se temos uma pirâmide, seu volume é a área da base vezes a altura dividia por . Assim, para o nosso plano genérico teríamos, por exemplo, a base como sendo o triângulo formado pela origem e pelos pontos que o plano corta os eixos e , e a altura seria o ponto que o plano corta o eixo .
Assim, como a área de um triângulo retângulo é um cateto vezes o outro sobre ,
Agora, multiplicando pela altura e por , pois é uma pirâmide,
E aí está! Nossa equação para o volume do tetraedro formado pelos eixos coordenados e o plano :D
Passo 3
Então vamos botar a mão na massa! Primeiro, precisamos encontrar a equação genérica para o plano tangente. Para isso, só precisamos encontrar o vetor gradiente da superfície e dizer que o produto escalar dele pelo vetor genérico é . Lembrando que esse vetor é a representação de todos os vetores que partem do ponto de tangência para o ponto do plano.
Fazendo as derivadas parciais, temos:
Então, o vetor gradiente no ponto
Passo 4
Beleza, agora chegou a hora de fazer o produto escalar:
Veja só, se passarmos para o lado direito os temos que tem as coordenadas e elevadas ao quadrado...
E sabemos que o ponto está na superfície , então, ! Assim, nossa equação para o plano tangente é:
Passo 5
Beleza, primeira etapa cumprida. Agora vamos ver o que esse plano tem a ver com o volume do tetraedro. Pelo o que o enunciado forneceu, se temos um plano de equação , então o volume do tetraedro é . Agora olha bem pro plano que encontramos no passo anterior. Se igualarmos os coeficientes , e desse plano do enunciado com o nosso plano, teremos que:
E o valor do termo independente será !
Assim, podemos escrever o volume como sendo:
Passo 6
Agora chegou a parte de minimizar essa nossa função, seguindo o nosso roteiro do Passo 1. Para isso, usaremos LaGrange, e a nossa restrição é a equação da superfície, por que ela que define os pontos possíveis do volume!
Assim,
Já sabemos qual é o vetor gradiente da superfície, . Vamos então calcular o vetor gradiente da função do volume:
Passo 7
Agora é resolver o sistema que tem as coordenadas do vetor gradiente de igualadas às coordenadas do vetor gradiente de multiplicadas por , mais a função restrição. Fica assim:
Feio né? Mas não iria colocar um sistema impossível da gente resolver, então vamos ver qual é a saída ;)
Bom, como o está aí só para ser isolado, por que na real ele não serve pra nada além de dizer que um vetor é múltiplo do outro, então vamos isolar ele nas equações:
Passo 8
Legal, agora temos essas três equações mais a equação da superfície. A ideia aqui vai ser arranjar uma relação entre uma das variáveis, por exemplo, e as outras duas. Assim, poderemos substituir tudo na última equação e ver o valor dessa variável.
Sem mais papo, vamos pegar a primeira e a segunda e igualar uma a outra:
Corta o , passa o de um lado pro outro e multiplica tudo por ,
Eleva os dois lados a e corta o ,
Como queremos a relação das outras com o , isola o :
Passo 9
Agora vamos igualar a primeira e a terceira equações:
Corta o e multiplica tudo por ,
Eleva os dois lados a e corta do ,
Isolando o , teremos:
Passo 10
Pronto! Temos tudo o que precisamos para substituir na quarta equação! Colocando e , teremos:
Como sabemos que estamos no primeiro octante, com todos os valores de , e positivos, ficamos com o valor positivo de , .
Passo 11
Finalmente! Reta final! Agora que temos o valor de , e sabemos que e ,
Colocando esses valores na equação do plano tangente,
Teremos:
Resposta
A equação do plano é: