Foi construída uma caixa com tampa, na forma de um paralelepípedo e com de volume. O material a ser utilizado nas laterais custa o dobro em relação ao que será utilizado na superfície do fundo. De acordo com sua resolução as dimensões da caixa que minimizam o custo do material são:
; ;
; ;
; ;
; ;
Passo 1
Eaew, tudo certinho contigo?
O enunciado nos dá uma caixa de volume , e ele quer calcular as dimensões da caixa que minimizaram o seu custo, fica atento que ele diz que o material que é utilizado no fundo custa duas vezes mais caro que o que é utilizado nas laterais. Para encontrar as dimensões da caixa, vamos lembrar como se calcula o volume de um paralelepípedo (ou caixa Kkkkkk), da seguinte forma
Se considerarmos uma caixa como a seguinte figura
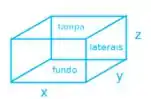
Vamos considerar que o fundo e a tampa são feitos do mesmo material! Então montar uma equação que determina nosso custo e utilizar o método dos multiplicadores de Lagrange para encontrar as dimensões que minimizam os custos. Vou apresentar cada coisa em seu momento para não ficar muito longo! Vem comigo!
Passo 2
Primeiro, vamos montar uma equação para nosso custo! Podemos relacionar o custo de cada parte com a área desta parte. Por exemplo, a área do fundo é dada por
Tanto o fundo como a tampa estão relacionados a um custo . A área das laterais, no entanto é composta pela área de todos os quatro lados da caixa, temos que
E como o enunciado nos diz, está relacionado a um custo . Desta forma, nosso custo total é equivalente à dar um peso as áreas laterais e dar um peso para a tampa e fundo, temos então
Beleza, com isso temos uma expressão que descreve o custo de nossa caixa! Agora vamos relembrar o método dos multiplicadores de Lagrange!
Passo 3
Para minimizar o custo da caixa, podemos utilizar os multiplicadores de Lagrange, construindo a seguinte função
Em que é uma restrição, em nosso caso dado por
ou seja, uma restrição sobre o volume da caixa. O objetivo do método, é formar um sistema de equações calculando pontos críticos das derivadas parciais, ou seja
Vamos fazer isso então! Vem comigo!
Passo 4
Primeiro, vamos usar a equação (3), junto com a equação (2) e a equação (4), para obter
Calculando as derivadas parciais e igualando a zero, temos
Vamos usar estas quatro equações para achar o valor de e então, encontrar o valor de cada uma de nossas variáveis! Vem comigo!
Passo 5
Primeiro vamos analisar a equação (5) e (6), da primeira, temos
Se evidenciarmos e então isolá-lo, temos
Invertendo o sinal no denominador para eliminar o sinal global, ficamos com
Da equação (6), se fizer o mesmo processo, vai chegar na mesma equação, saca só
E, portanto
O que resulta em . Vamos utilizar este resultado na equação (7) para encontrar , bora lá!
Passo 6
Temos colocando a equação (9) na equação (7), que
Note que usei que para somar os dois primeiros termos, e pelo mesmo motivo, o último termo fica ao quadrado. Podemos multiplicar os dois lados por e dividir os dois lados por , para obter
Se multiplicarmos mais uma vez por , temos
Isolando passando dividindo, temos
E utilizando (10) na equação (9), temos que
Maaaravilha! Agora só falta utilizarmos e na equação para acharmos quem é e temos tudo que precisamos para saber qual é o nosso ponto! Saca só!
Passo 7
Colocando e em , temos que
Multiplicando as frações, temos
Se tirar a raiz cúbica, temos que
O que nos resulta da equação e , que
E
E estas são as dimensões de nossa caixa! Maaaravilha! A questão foi isso! Te vejo na próxima! Tchau Tchau!