Multiplicadores de Lagrange
Seja e seja a curva
(a) Calcule os valores de máximo e mínimo global de restrita à curva .
(b) Determine em qual(is) ponto(s) de o valor máximo de é atingido e em qual(is) ponto(s) de o valor mínimo de é atingido.
Passo 1
(a) Essa é uma típica questão de Lagrange, basta seguir o passo a passo!
Vamos primeiro definir . Buscamos o máximo e o mínimo de restrita à curva . Então, pelo método dos multiplicadores de Lagrange, vamos ter o sistema seguinte:
Passo 2
Beleza, agora vamos achar esses gradientes, calculando as derivadas parciais:
Logo:
Então, o gradiente da vai ser:
E pra vamos ter, pela regra da cadeia:
E:
E o gradiente vai dar:
Passo 3
Show! Agora vamos montar o nosso sistema com o que achamos:
Da segunda equação, tiramos:
Bora analisar separadamente os 2 casos:
Passo 4
Se , vamos ter:
A primeira equação do sistema vai ficar:
- Se , pela terceira equação do sistema:
- E se :
Portanto, achamos os pontos , e . Mas isso foi assumindo que lembra? Ainda temos o caso . Então partiu!
Passo 5
Se vamos ter:
Portanto, achamos os pontos e . Como já tínhamos achado o ponto , vamos guardar só o primeiro.
Então o ponto também é candidato a ponto de máximo ou mínimo de em .
Passo 6
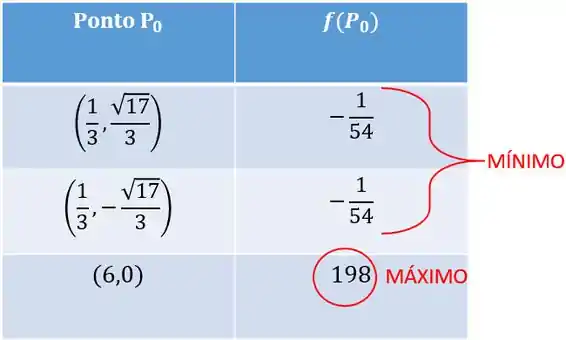
Agora basta calcular o valor de em cada ponto que achamos e achar os valores máximo e mínimo. Lembrando que os nossos candidatos são os pontos:
;
E que a função é definida por:
Portanto, os valores de máximo e mínimo globais de restrita à curva , são, respectivamente, e . Já podemos emendar com a resposta da letra (b):
(b) O valor máximo é atingido no ponto e o valor mínimo nos pontos e .
Resposta
