Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Substituição Simples

Ver Teoria
Exercício 891234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283848586878890919293949596979899100

Enunciado

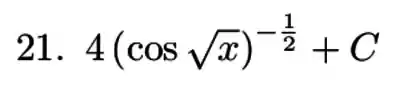
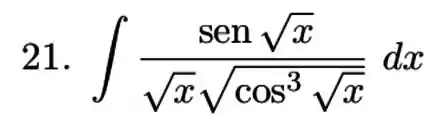
Passo 1

PARA TUDO, PORQUE TEMOS UM MONSTRO AQUI! Relaxa, que é só arrumar que ele ficará menos feio 😊

Vamos reescrever essa integral assim:

∫ s e n x x c o s ³ ( x ) d x = ∫ cos - 3 2 ( ⁡ x 1 2 ) s e n x 1 2 x - 1 2 d x

Tudo bem, que ele não tá lááá a coisa mais linda, mas perceba que:

d x 1 2 d x = 1 2 x - 1 2

E ainda:

d ( cos ⁡ x - 1 2 ) d x = 1 2 cos ⁡ x - 3 2 s e n ( x )

Tem coisas bem parecidas, não concorda? Bom, nessa questão vamos usar o método da substituição! O truque aqui é:

u = cos ⁡ x - 1 2 → d u = 1 2 cos ⁡ x - 3 2 s e n x 1 2 x - 1 2 d x

Perceba que para encontrar o d u apenas usamos a derivação em cadeia. Então, arrumando aquilo:

d u = 1 2 cos ⁡ x - 3 2 s e n x 1 2 x - 1 2 d x = d u = 1 4 s e n x x cos ⁡ x 3 d x

Passo 2

Substituindo na integral:

∫ s e n x x c o s ³ ( x ) d x = ∫ 4 d u

Passo 3

Resolvendo a integral:

∫ 4 d u = 4 u + C

Passo 4

Lembrando de algo MUITO IMPORTANTE! u foi uma variável que você criou, então precisamos voltar para a variável do problema, ok?

u = cos ⁡ x - 1 2

4 u + C = 4 cos ⁡ x - 1 2 + C

Prontinho! Agora tá certinho. 😊

Resposta

Exercícios de Livros Relacionados

Calcule a integral.int x^3 (x - 1)^(- 4) d x
Calcule a integral fazendo a substituição dada. ∫ cos ⁡ 3 x d x , u = 3 x
32. int (d t)/((2 + t)^2)
Use a fórmula de substituição do Teorema 7 para calcular as integrais nos Exercícios 1-46. ∫ π 3 π / 2 cot 5 ⁡ θ 6 sec 2 ⁡ θ 6 d θ
Calcule a integralint (sec x cos 2 x)/(s e n x + sec x) d x