UNICAMP, Sem Campus, Cálculo 1, Listas de Cálculo 1 - Profº Ricardo Martins - Lista sobre Integrais, Questão 4.7
4.7. Calcule e explique por que que esta integral pode ser usada para calcular a área do círculo unitário.
Passo 1
E aí! Suave na nave?! Tá difícil essa questão? Relaxa que a gente vai te ajudar!
Nesse problema queremos obter a integral e explicar por que essa integral pode ser usada para calcular a área do círculo unitário.
E aí, tem alguma ideia do que fazer? 🤔
Para explicar o motivo dessa integral resultar na área de um círculo unitário, a melhor maneira é desenvolver a função de integração.
Bora ver como é! 😎
Passo 2
Igualando a função de integração a , temos
Perceba que essa função é exatamente igual a equação da circunferência centrada na origem de raio .
Como temos
O gráfico dessa função seria apenas a parte positiva de , ou seja, a parte de cima da circunferência (isso porque não temo como a raiz de um número resultar em um valor negativo).
Esboçando o gráfico da função e hachurando a região de integração entre e , vamos ter
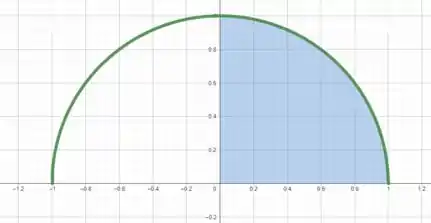
Perceba que a região de integração corresponde a da área do círculo, assim, como o problema é vezes essa integral, o resultado é a área de um círculo de raio completo
O que achou? Foi de boa? Responde aí! 😊
