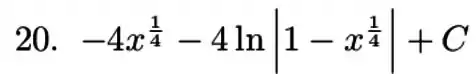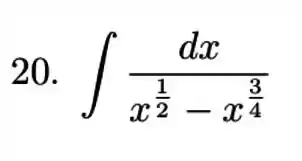
Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Substituição Simples

Ver Teoria
Exercício 101123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Passo 1

Essa ideia de utilizar a substituição x = y n serve para tirar nossa variável das raízes. Então qual n devemos usar?

Temos uma raiz quarta e uma raiz quadrada, então nosso n deve ser 4.

x = y 4

Passo 2

Escolhida a nossa substituição, vamos calcular a derivada

x = y 4

d x = 4 y 3 d y

E aplicar a substituição na integral

∫ d x x 1 / 2 - x 3 / 4   = ∫ 4 y 3 y 4 1 / 2 - y 4 3 / 4 d y

∫ d x x 1 / 2 - x 3 / 4   = ∫ 4 y 3 y 2 - y 3 d y

Podemos manipular um pouco melhor nossa integral

∫ d x x 1 / 2 - x 3 / 4   = 4 ∫ y 3 y 2 ( 1 - y ) d y

∫ d x x 1 / 2 - x 3 / 4   = 4 ∫ y ( 1 - y ) d y

Passo 3

Agora nos resta resolver a integral

4 ∫ y 1 - y d y = - 4 ∫ y y - 1 d y

Para isso podemos usar o método da substituição

u = y - 1

d u = d y

Aplicando na integral ficamos com

- 4 ∫ y y - 1 d y = - 4   ∫ u + 1 u d u

= - 4 ∫ u u d u + ∫ 1 u d u

= - 4 ∫ d u + ∫ 1 u d u

= - 4 - 4 ln ⁡ u + C

Desfazendo a substituição

u = y - 1

- 4 ∫ y y - 1 d y = - 4 y - 1 - 4 ln ⁡ y - 1 + C

Passo 4

Ok! Resolvemos a integral, mas não podemos esquece que nossa variável inicial é x e não y .

Vamos rearranjar um pouco nosso resultado e desfazer a substituição

- 4 ∫ y y - 1 d y = - 4 y - 1 - 4 ln ⁡ y - 1 + C

= - 4 y + 4 - 4 ln ⁡ y - 1 + C

Esse 4 pode ir fazer parte da nossa constante

- 4 ∫ y y - 1 d y = - 4 y - 4 ln ⁡ y - 1 + C

∫ d x x 1 / 2 - x 3 / 4   = - 4 y - 4 ln ⁡ y - 1 + C

Agora vamos desfazer a nossa substituição

x = y 4

y = x 4

∫ d x x 1 / 2 - x 3 / 4   = - 4 x 4 - 4 ln ⁡ x 4 - 1 + C

Prontinho!

Resposta

Exercícios de Livros Relacionados

Calcule a integral.int x^3 (x - 1)^(- 4) d x
Calcule a integral fazendo a substituição dada. ∫ cos ⁡ 3 x d x , u = 3 x
32. int (d t)/((2 + t)^2)
Use a fórmula de substituição do Teorema 7 para calcular as integrais nos Exercícios 1-46. ∫ π 3 π / 2 cot 5 ⁡ θ 6 sec 2 ⁡ θ 6 d θ
Calcule a integralint (sec x cos 2 x)/(s e n x + sec x) d x