UNICAMP, Sem Campus, Cálculo 1, Listas de Cálculo 1 - Profº Ricardo Martins - Lista sobre Integrais, Questão 2.7
2.7. Calcule
(Dica: a função é ímpar, pense no seu gráfico e na área abaixo dele)
Passo 1
Iae, como vai? Essa questão está um pouco complicada? Fique tranquilo que vamos tentar te ajudar. 😎👍
Nesse problema estamos interessados em obter a integral de entre e .
Parece tranquilo? 🤔
Ainda no enunciado, foi dito que a função de integração é ímpar e seria interessante olhar para o tráfico de e na área abaixo dele.
Ok, mas o que é uma função ímpar? 👀
Para determinar se uma função é ímpar, você precisa verificar se ela atende à propriedade de simetria ímpar, ou seja, se a função é igual a para todos os valores de no domínio da função.
Sacou? Bora começar! 😉
Passo 2
Temos que a função de integração é
Perceba que no denominador, as ordens de são sempre pares, então se for positivo ou for negativo, o sinal será sempre o mesmo.
Já no numerador, temos , sabemos que o gráfico de possui simetria ímpar entre .
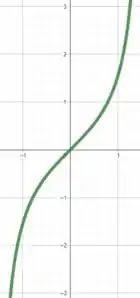
Ou seja, realmente é uma função ímpar.
Como regra, quando temos uma função ímpar integrada em um intervalo simétrico, o resultado dessa integral é
Como nossa função é ímpar e o intervalo simétrico, temos
E todos viveram felizes para sempre. Fim! 😉 Entendeu tudo? Responde Aí
