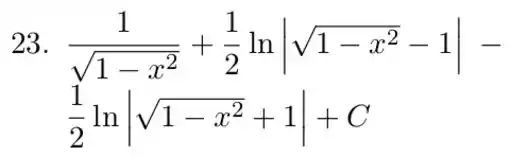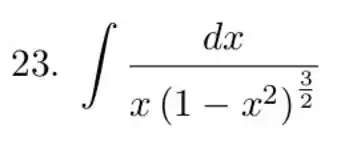
Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Substituição Trigonométrica

Ver Teoria
Exercício 281234567891011121314151617181920212223242526272930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Passo 1

Precisamos resolver

∫ d x x 1 - x 2 3 2   = ∫ d x x ( 1 - x 2 ) 1 - x 2

Podemos utilizar a substituição

u = 1 - x 2

d u =   - x 1 - x 2 d x

Então

u 2 = 1 - x 2

x 2 = 1 - u 2 = - ( u 2 - 1 )

Aplicando na integral ficamos com

∫ d x x 1 - x 2 3 2   = ∫ d u u 2 ( u 2 - 1 )

Passo 2

Perceba que

∫ d u u 2 ( u 2 - 1 ) = ∫ d u u 2 ( u - 1 ) ( u + 1 )

Aqui, podemos utilizar frações parciais para nos ajudar a resolver

1 u 2 ( u - 1 ) ( u + 1 ) = A u 2 + B ( u - 1 ) + C u + 1

Trabalhando a expressão ficamos com

1 u 2 ( u - 1 ) ( u + 1 ) = A ( u 2 - 1 ) u 2 ( u - 1 ) ( u + 1 ) + B u 2 ( u + 1 ) u 2 ( u - 1 ) ( u + 1 ) + C u 2 ( u - 1 ) u 2 ( u - 1 ) ( u + 1 )

1 = A u 2 - A + B u 3 + B u 2 + C u 3 - C u 2

u 3 B + C + u 2 A + B - C - A

Logo

A = - 1 ;     B = 1 2 ;     C = - 1 2

Aplicando na integral vamos ficar com

∫ d u u 2 ( u - 1 ) ( u + 1 ) = - ∫ d u u 2 + 1 2 ∫ d u u - 1 - 1 2 ∫ d u u + 1

Passo 3

Integrando teremos

∫ d u u 2 ( u - 1 ) ( u + 1 ) = 1 u + 1 2   l n   u - 1   - 1 2   l n   u + 1 + C  

E desfazendo a nossa substituição

u = 1 - x 2

∫ d x x 1 - x 2 3 2   = 1 1 - x 2 + 1 2   l n   1 - x 2 - 1   - 1 2   l n   1 - x 2 + 1 + C  

Pronto! Resolvido!

Resposta

Exercícios de Livros Relacionados

Encontre o volume do sólido obtido pela rotação em torno da reta x = 1 da região sob a curva y = 1 - x 2 , 0 ≤ x ≤ 1 .
Calcule a integral usando a substituição trigonométrica indicada. Esboce e coloque legendas no triângulo retângulo associado. ∫ x 3 9 - x 2 d x ; x = 3 sin ⁡ θ
Calcule a integral indefinida:int (x^2)/(sqrt(2 - x^2)) d x
Calcule a integral indefinida:int (5 x + 4)/(x^3 sqrt(x^2 + 1)) d x
Calcule a integralint (1)/(x^2 sqrt(4 x^2 - 1)) d x