Calcule as seguintes integrais indefinidas:
Passo 1
O primeiro passo em questões de integral é identificar o método de integração que devemos utilizar para conseguir resolver ou que aparentemente pode nos levar à solução de forma mais fácil.
Tá, essa raiz quadrada com somado a constante é um indicador direto do método da Substituição Trigonométrica, você concorda.
Na Substituição Trigonométrica poderemos encontrar 3 casos:
Quando você cai num método de integração dividido em casos, o próximo passo é identificar de qual caso se trata para, a partir daí, direcionar a forma de resolver.
E qual dos três casos vamos usar? Temos uma expressão do tipo , onde seria igual a 3.
Então, a substituição que devemos fazer nesse caso é:
Passo 2
Agora vamos partir para a resolução propriamente dita. Já identificamos qual caso usar. O próximo passo é identificar quem é o e, a partir disso, calcular e substituir na integral.
Temos , onde
Portanto, a substituição que devemos fazer será:
Derivando , encontramos o :
Agora, vamos substituir na integral:
Vamos tirar de dentro da integral tudo o que for constante.
Na raiz quadrada do denominador, a gente pode colocar o 3 em evidência para depois utilizar uma identidade trigométrica para simplificar a integral.
Agora sim, fica mais de identificar a identidade trigonométrica e fazer a substituição.
Passo 3
Bom, depois de substituir tudo e simplificar o máximo possível, devemos resolver a integral em . E para resolver essa integral aqui? #Como faz?
Sabemos que se trata de uma integral trigonométrica. Essa integral trigonométrica envolve tangente e secante, sendo o expoente da tangente ímpar. Nessa situação, a gente guarda um , que é derivada da secante, e abre o resto das tangentes em secantes:
Passo 4
Fazendo a seguinte substituição simples:
Vai ficar:
Passo 5
Bom, agora que já resolvemos a integral em . Agora temos que voltar para . Então montamos aquele triângulo maroto para des-substituir o para , lembrando que no caso da tangente, o triângulo fica com essa cara aqui, ó:
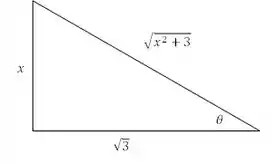
A partir dessa triângulo, tiramos todas as relações de que precisamos. Nesse caso, só precisamos de
Substituindo isso no resultado em que havíamos encontrado e lembrando que é uma integral indefinida, portanto, não devemos esquecer a constante , beleza? Se liga aí para não dar bobeira!