Resolva as integrais seguintes:
f)
Passo 1
Fala, galera! Vamos resolver essa questão.
O enunciado pediu pra gente resolver a integral indefinida na forma:
Galera, lembrete:
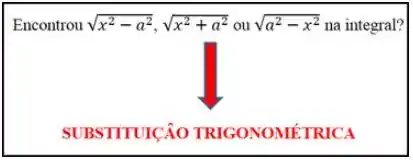
No nosso caso, temos , onde (a gente sempre considera só a raiz positiva nesses casos). Pra essa raiz, nós usamos a substituição:
Pra encontrar o basta derivar:
Agora basta a gente substituir e na nossa integral.
Vamos lá!
Passo 2
Primeiro, vamos olhar a substituição só na raiz:
Elevando ao quadrado:
Tirando o da raiz e usando a identidade trigonométrica:
Temos:
Agora vamos colocar tudo na integral.
Passo 3
Simplificando:
Mas nós temos as identidades:
Substituindo na integral:
Pra resolver essa integral, vamos chamar Assim, , e temos:
Voltando pra nossa variável :
Mas lá em cima a gente definiu , então . Substituindo no nosso resultado:
Ainda dá pra gente deixar isso com uma cara mais bonitinha, usando a identidade:
Assim, temos:
E chegamos em:
Prontinho, galera! Até a próxima! 😉