Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Substituição Trigonométrica

Ver Teoria
Exercício 671234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Use substituição trigonométrica para calcular a integral dada:

∫ 0 2 3 x 2 9 - x 2 3 2 d x

Passo 1

Vamos manipular um pouco nossa integral

∫ 0 2 3 x 2 9 - x 2 3 / 2 d x = ∫ 0 2 3 x 2 ( 9 - x 2 ) 9 - x 2 d x

Precisamos encontrar qual caso de substituição se aplica na nossa integral

9 - x 2

Repare que está no mesmo formato de

a 2 - x 2

Nesse caso

x = a sen ⁡ θ

Então teremos

x = 3 sen ⁡ θ

Passo 2

A próxima coisa a se fazer é encontrar d x , derivando

x = 3 sen ⁡ θ

d x = 3 cos ⁡ θ d θ

Passo 3

Agora precisamos substituir x   e d x na nossa integral.

∫ 0 2 3 x 2 ( 9 - x 2 ) 9 - x 2 d x = ∫ 0 2 3 ( 9 sen 2 ⁡ θ ) ( 9 - 9 sen 2 ⁡ θ ) 9 - 9 sen 2 ⁡ θ   3 cos ⁡ θ d θ

∫ 0 2 3 x 2 ( 9 - x 2 ) 9 - x 2 d x = ∫ 0 2 3 ( 9 sen 2 ⁡ θ ) 9 ( 1 - sen 2 ⁡ θ ) 9 ( 1 - sen 2 ⁡ θ )   3 cos ⁡ θ d θ

Vamos fazer a substituição cos 2 ⁡ θ = 1 - sen 2 ⁡ θ

∫ 0 2 3 x 2 ( 9 - x 2 ) 9 - x 2 d x = ∫ 0 2 3 ( 9 sen 2 ⁡ θ ) 9 cos 2 ⁡ θ 9 cos 2 ⁡ θ   3 cos ⁡ θ d θ

∫ 0 2 3 x 2 ( 9 - x 2 ) 9 - x 2 d x = ∫ 0 2 3 ( 9 sen 2 ⁡ θ ) 9 cos 2 ⁡ θ 3 cos ⁡ θ   3 cos ⁡ θ d θ

∫ 0 2 3 x 2 ( 9 - x 2 ) 9 - x 2 d x = 3 ∫ 0 2 tan 2 ⁡ θ d θ

Sabemos que tan 2 ⁡ θ = sec 2 ⁡ θ - 1

∫ 0 2 3 x 2 ( 9 - x 2 ) 9 - x 2 d x = 3 ∫ 0 2 sec 2 ⁡ θ d θ - 3 ∫ 0 2 d θ

Passo 4

O próximo passo é resolver a integral

∫ 0 2 3 x 2 ( 9 - x 2 ) 9 - x 2 d x = 3 ∫ 0 2 sec 2 ⁡ θ d θ - 3 ∫ 0 2 d θ

∫ sec 2 ⁡ θ d θ = tan ⁡ θ

∫ 0 2 d θ = θ

∫ 0 2 3 x 2 ( 9 - x 2 ) 9 - x 2 d x = 3 tan ⁡ θ - 3 θ 0 2

Passo 5

Mas não podemos dar a resposta em função de θ , precisamos voltar para x . Para isso vamos precisar do triângulo retângulo. Sabemos que

sen ⁡ θ = x 3

Então

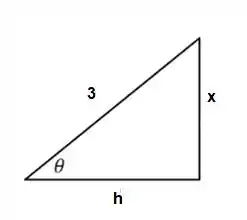
Usando Pitágoras podemos encontrar o cateto adjacente

9 = x 2 + h 2

h = 9 - x 2

Com isso, encontramos

θ = arcsen ⁡ x 3

tan ⁡ θ = x 9 - x 2

Substituindo na nossa integral

∫ 0 2 3 x 2 ( 9 - x 2 ) 9 - x 2 d x = 3 tan ⁡ θ - 3 θ 0 2

∫ 0 2 3 x 2 ( 9 - x 2 ) 9 - x 2 d x = 3 x 9 - x 2 - 3 arcsen ⁡ x 3 0 2

Aplicando os limites de integração

∫ 0 2 3 x 2 ( 9 - x 2 ) 9 - x 2 d x = 6 5 5 - 3 arcsen ⁡ 2 3

Resposta

∫ 0 2 3 x 2 9 - x 2 3 2 d x = 6 5 5 - 3 arcsen ⁡ 2 3

Exercícios de Livros Relacionados

Encontre o volume do sólido obtido pela rotação em torno da reta x = 1 da região sob a curva y = 1 - x 2 , 0 ≤ x ≤ 1 .
Calcule a integral usando a substituição trigonométrica indicada. Esboce e coloque legendas no triângulo retângulo associado. ∫ x 3 9 - x 2 d x ; x = 3 sin ⁡ θ
Calcule a integral indefinida:int (x^2)/(sqrt(2 - x^2)) d x
Calcule a integral indefinida:int (5 x + 4)/(x^3 sqrt(x^2 + 1)) d x
Calcule a integralint (1)/(x^2 sqrt(4 x^2 - 1)) d x