Calcule as seguintes integrais:
Passo 1
A primeira coisa que a gente pensa ao olhar para essa integral é a integração por partes, concorda? Estamos trabalhando com funções muito distintas: logaritmo não tem nenhuma relação direta com polinômios. Pela regrinha do LIATE nós devemos escolher como nosso da integração por partes o , o resto do termo será . A partir disso, tudo consiste em aplicar a fórmula desse método:
Essa integral do a gente pode fazer por substituição simples do .
Agora aplicamos aquela fórmula da integral por partes:
Agora sobrou uma outra integral, resolvemos ela para finalizar!
Passo 2
E agora? Repara bem: tenho uma raiz com um ali. Isso aí não tá pedindo uma substituição trigonométrica?
Temos uma expressão do tipo .
Então, a substituição que devemos fazer nesse caso é:
Passo 3
Agora vamos partir para a resolução propriamente dita. Já identificamos qual caso usar. O próximo passo é identificar quem é o e, a partir disso, calcular e substituir na integral.
Temos
Portanto, temos:
Substituindo na integral:
Repara que a tangente sai da raiz como módulo!
Porém, se olharmos a definição desse caso em que substituímos , veremos que definimos o intervalo de como . Nesse intervalo, . Como a tangente será sempre positiva e seu módulo será igual a ela mesma:
Passo 4
Agora devemos resolver a integral na variável . Essa integral é tranquilinha:
Passo 5
Resolvemos a integral em . Agora temos que voltar para . Então montamos aquele triangulozinho básico para des-substituir o para , lembrando que no caso da secante, o triângulo fica com essa cara aqui, ó:
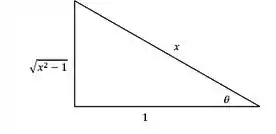
Nesse caso, precisamos calcular e o próprio :
Como fizemos a substituição , podemos tirar direto a seguinte relação:
Substituindo isso no resultado em que havíamos encontrado e lembrando que é uma integral definida, portanto, não devemos esquecer a constante , temos:
Lembrando que essa era só a integral em que caímos depois. A integral que queríamos resolver no enunciado era essa aqui:
Portanto: