Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Substituição Trigonométrica

Ver Teoria
Exercício 651234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636466676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Calcule a seguinte integral

∫ x 3 4 - x 2 d x

Passo 1

Ali a gente tem uma raiz com a cara a 2 - x 2 , com a = 2 , por isso a gente pode pensar em usar a substituição trigonométrica:

x = a   s e n   θ = 2   s e n   θ

d x d θ = 2 cos ⁡ θ ∴ d x = 2 cos ⁡ θ   d θ

A integral fica assim:

∫ ( 2   s e n   θ ) 3 4 - 2   s e n   θ 2 d x = ∫ ( 2   s e n   θ ) 3 4 - 2   s e n   θ 2 2 cos ⁡ θ d θ

Passo 2

Vamos reescrever esse integrando para calcular a integral. Lembrando de uma identidade trigonométrica:

s e n 2 θ + cos 2 ⁡ θ = 1 ∴ cos 2 ⁡ θ = 1 - s e n 2 θ

Podemos reescrever a integral assim:

∫   8   s e n 3 θ 4 - 4   s e n 2 θ ⋅ 2 cos ⁡ θ d θ = ∫ 8   s e n 3 θ 4 1 -   s e n 2 θ ⋅ 2 cos ⁡ θ d θ = ∫   8   s e n 3 θ 4 cos 2 ⁡ θ ⋅ 2 cos ⁡ θ d θ

= ∫   8   s e n 3 θ 2 cos ⁡ θ ⋅ 2 cos ⁡ θ d θ = 8 ∫ s e n 3 θ d θ

Passo 3

Agora a gente calcula essa integral. Como temos um seno elevado a um expoente ímpar, a gente vai o reescrever, como um produto, deixando um terminho de seno sozinho, assim

s e n 3 θ = s e n 2 θ   s e n   θ

Aí vamos usar aquela identidade trigonométrica de novo:

s e n 2 θ + cos 2 ⁡ θ = 1 ∴ s e n 2 θ = 1 - cos 2 ⁡ θ

Aí o nosso integrando pode ficar assim:

s e n 3 θ = s e n 2 θ   s e n   θ = 1 - cos 2 ⁡ θ   s e n   θ

Substituindo isso na nossa integral:

8 ∫ s e n 3 θ d θ = 8 ∫ 1 - cos 2 ⁡ θ   s e n   θ d θ

Percebe que agora a gente tem uma expressão estranha em cos ⁡ θ , mas temos um seno sozinho ali fofo. Isso é uma dica para usarmos a substituição simples

u = cos ⁡ θ ,     d u d θ = - s e n   θ ∴ d u - 1 = s e n   θ   d θ

∴

8 ∫ 1 - cos 2 ⁡ θ   s e n   θ d θ = 8 ∫ 1 - u 2 d u - 1 = - 8 ∫ 1 - u 2 d u = 8 - u + u 3 3

Voltando para θ :

8 ∫ s e n 3 θ d θ = 8 ∫ 1 - cos 2 ⁡ θ   s e n   θ d θ = 8 - u + u 3 3 = 8 - cos ⁡ θ + cos 3 ⁡ θ 3

Passo 4

Mas a nossa integral estava em função de x Então a gente tem que voltar para essa variável. Usamos a substituição:

x = 2   s e n θ ∴ x 2 = s e n   θ ∴ θ = a r c s e n   x 2

Desenhando o triângulo retângulo com esse ângulo θ , que tem x / 2 como seno, e usando Pitágoras para achar o lado que falta:

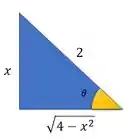
Daí a gente pode tirar que:

  cos ⁡ θ = 4 - x 2 2

∫ x 3 4 - x 2 d t = 8 ∫ s e n 3 θ d θ = 8 - cos ⁡ θ + cos 3 ⁡ θ 3 = 8 - 4 - x 2 2 + 1 3 4 - x 2 2 3

E a gente não pode esquecer do C , já que temos uma integral indefinida

∫ x 3 4 - x 2 d t = 8 - 4 - x 2 2 + 1 3 4 - x 2 2 3 + C

Resposta

8 - 4 - x 2 2 + 1 3 4 - x 2 2 3 + C

Exercícios de Livros Relacionados

Encontre o volume do sólido obtido pela rotação em torno da reta x = 1 da região sob a curva y = 1 - x 2 , 0 ≤ x ≤ 1 .
Calcule a integral usando a substituição trigonométrica indicada. Esboce e coloque legendas no triângulo retângulo associado. ∫ x 3 9 - x 2 d x ; x = 3 sin ⁡ θ
Calcule a integral indefinida:int (x^2)/(sqrt(2 - x^2)) d x
Calcule a integral indefinida:int (5 x + 4)/(x^3 sqrt(x^2 + 1)) d x
Calcule a integralint (1)/(x^2 sqrt(4 x^2 - 1)) d x