UFABC – Sem Campus – Funções de Uma Variável – Listas – Listas FUV – GRADMAT – Lista 9 – Técnicas de Integração I – Questão 11 – Alternativa a)
Calcule as integrais usando substituição trigonométrica. Esboce o triângulo retângulo associado.
Passo 1
Oiiie, tudo certinho? Bora que bora?
Eu sei que substituição trigonométrica parece o demônio! Mas vamos tentar fazer devagarzinho e ver se surge uma luz! Utilizar este método é uma questão de identificar casos específicos! Nesta questão temos o seguinte caso:
Em que . Para esta situação é conveniente usar a substituição:
Vamos trabalhar um pouco em cima disso! Bora lá!
Passo 2
Utilizando a substituição em nossa integral, temos que:
Parece que piorou neh? Mas na verdade está melhor! Vamos lembrar que:
E que:
De forma que:
Belezinha! Só precisamos reescrever isto mais um pouquinho! Vem comigo!
Passo 3
Vamos lembrar que:
Ou seja,
Agora ficou mais simples hehehehe, só precisamos identificar a primitiva como:
Só precisamos fazer uma última coisinha! E é voltar para a variável original! Vamos analisar o triângulo retângulo para isso! Saca só!
Passo 4
Temos que:
E, utilizando Pitágoras para obter o cateto oposto, temos:
E nosso triângulo retângulo tem a forma:
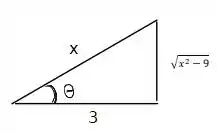
Beleza, vamos usar esse triângulo para encontrar a nossa resposta! Saca só!
Passo 5
Desta forma, temos que:
Maravilha! Nossa resposta final é então:
Feito! Bora para a próxima hehehehe! Até daqui a pouco!
