Integração por Substituição Trigonométrica
Calcule as seguintes integrais:
Passo 1
Nessa integral aí aparece um termo que lembra o formato de uma substituição trigonométrica:
Nesse caso, quando o formato do termo é a substituição seria de :
Jogando isso na integral ficamos assim:
Passo 2
Temos que desfazer a substituição. Para isso, a boa é desenhar um triângulo retângulo onde temos um ângulo cuja tangente vale , ou melhor, . Dado esse triângulo, determinamos quanto valeria o seno do mesmo ângulo:
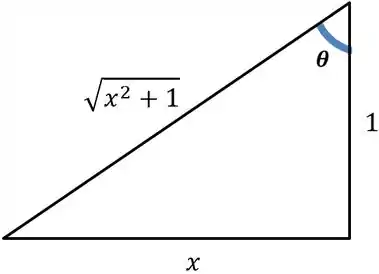
Por Pitágoras, descobrimos a hipotenusa desse triângulo com a tangente de sendo . Nele, o seno desse ângulo será dado assim:
Enfim, eis a nossa resposta:
Resposta
Exercícios de Livros Relacionados
Encontre o volume do sólido obtido pela rotação em torno da reta x = 1 da região sob a curva y = 1 - x 2 , 0 ≤ x ≤ 1 .
Calcule a integral usando a substituição trigonométrica indicada. Esboce e coloque legendas no triângulo retângulo associado. ∫ x 3 9 - x 2 d x ; x = 3 sin θ
Calcule a integral indefinida:int (x^2)/(sqrt(2 - x^2)) d x
Calcule a integral indefinida:int (5 x + 4)/(x^3 sqrt(x^2 + 1)) d x
Calcule a integralint (1)/(x^2 sqrt(4 x^2 - 1)) d x