Q01c) Calcule as integrais abaixo
Passo 1
Essa integral é bem feinha né? Tem raiz, polinômio dentro e fora dela e como se não bastasse, a raiz ainda ta no denominador! Mas olha só, eu tenho algo do tipo dentro da raiz. Quando é assim, da pra gente brincar de Pitágoras:
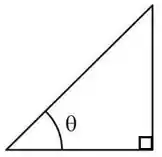
Falta só eu dar nome aos bois. Ou melhor, aos catetos e a hipotenusa. Como tio Pitágoras falou pra gente que:
Pra uma raiz e um sinal de menos dentro dela aparecer, a única forma é manipulando:
Agora ficou um pouco com a cara do que temos na raiz né. Vamos ter:
E logo:
Mas também:
Agora é só a gente por tudo dentro do triângulo retângulo:
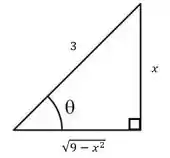
E acredite ou não, esse triângulo simpático vai ajudar bastante a gente! Uma coisa importante sobre essa forma de resolver é que as vezes a escolha das posições dos catetos atrapalha a gente. Não tem jeito, é tentativa e erro. Essa posição ai já vai nos dar o pulo do gato.
Passo 2
Bem, já que temos o triângulo auxiliar, a partir dele e o ângulo , conseguimos tirar relações trigonométrica. Por exemplo:
E logo:
Agora é só substituir na integral. Mas antes pra achar a expressão de em função de , vamos derivar a segunda linha:
Juntando tudo, vamos ter:
Opa, restou só uma integral! Uma até bem direta. Sabe porque? Porque tem uma relação trigonométrica i.m.p.o.r.t.a.n.t.í.s.s.i.m.a que diz que:
Substituindo então, temos:
Passo 3
Fechamos a integração, o resultado deu:
Vai faltar só a gente voltar pra variável original. E é pra isso que temos nosso triângulo auxiliar:
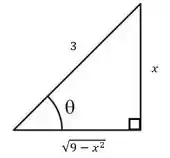
Veja bem, se tínhamos feito a substituição:
Vamos ter:
Agora, note que:
E o seno e o cosseno dá pra tirar do triângulo em! vamos ter:
Substituindo isso vamos ter: