Calcule a integral
Passo 1
Essa integral, a princípio, não tem muita cara de nada que a gente sabe resolver, né? E aí? Nesses casos, a gente tenta jogar uma substituição simples marota para ver se dá uma simplificada e ver se chegamos em algo com uma carinha melhor.
Vamos simplificar esse bicho feio aí? Repara comigo que eu tenho um no denominador e tenho, dentro da raiz, um . Cara, se eu jogar o para cima, basta inverter o sinal do expoente:
Fala sério, a partir daqui, eu posso chamar essa coisa feia de , né?
Mandei essa substituição simples nessa integral. A nova cara é essa:
Passo 2
E agora? Tá vendo que tenho uma raiz com um ali? Vai dizer que isso não te lembra nada? Não parece que isso vai sair por substituição trigonométrica?
Então... agora que você já sabe qual é o método de integração que deve te conduzir à luz, identifique o caso e seja feliz!
Bom, temos uma expressão do tipo .
Então, a substituição que devemos fazer nesse caso é:
Passo 3
Agora vamos partir para a resolução propriamente dita. Já identificamos qual caso usar. O próximo passo é identificar quem é o e, a partir disso, calcular e substituir na integral.
Temos
Portanto, temos:
Substituindo na integral:
Passo 4
Agora devemos resolver a integral na variável . Essa integral é molezinha, amigo, tirar doce de criança:
Passo 5
Bom, agora que já resolvemos a integral em . Agora temos que voltar para . Então montamos aquele triângulo maroto para des-substituir o para , lembrando que no caso do seno, o triângulo fica com essa cara aqui, ó:
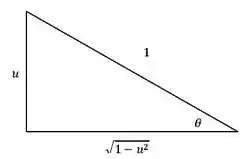
A partir dessa triângulo, tiramos todas as relações de que precisamos. Nesse caso, só precisamos do valor de . Repare que a relação é a que vai dar a expressão mais simples:
Eu poderia ter escolhido calcular o cosseno ou tangente, mas esse foi o que deu a expressão mais simples, por isso a escolhi.
Substituindo isso no resultado em que havíamos encontrado e lembrando que é uma integral definida, portanto, não devemos esquecer a constante , beleza? Se liga aí para não dar bobeira!
Chamei a constante aí em cima de porque essa ainda não é a resposta definitiva. Voltamos para mas a integral que tínhamos inicialmente era em . Esse aí veio daquela substituição esperta que fizemos para faciliar nossa vida.
Agora temos que voltar para . Lembrando que fizemos :
- ''