UFRJ. Cálculo 1. Prova P2. 2022.1. Questão 1c.
1) Calcule as integrais.
c)
Passo 1
Fala aí! Tudo certinho? Esta questão está um pouco complicada? Relaxa que vamos tentar te ajudar. 😎
Essa é uma questão bem direta! Foi dito que temos apenas que calcular a integral da função , parece fácil? 😉
Como podemos calcular essa integral? 🤔🤔
Essa função de integração do jeito que veio ao mundo não é muito fácil de ser integrada, mas podemos fazer algumas mudanças que não impactam na dinâmica da função.
Como por exemplo podemos usar as relações trigonométricas para conseguirmos simplificar a função aplicando o método de integração por substituição.
Preparado? Bora começar! 😁
Passo 2
Primeiro, vamos lembrar do teorema fundamental do cálculo que diz que a derivada de é igual a .
Vamos usar essa ideia para aplicar o método de substituição na integral.
Pelas relações trigonométricas da e da , temos que
Ou seja
Olhando para nossa função de integração, temos
Substituindo por , vamos obter
Assim, nossa integral fica como
Entendeu?
Passo 3
Parece que piorou a nossa situação, não é? 👀
Mas olha só, se aplicarmos o método de substituição fazendo , vamos ter que
Portanto e então aplicando as substituições.
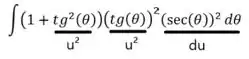
Simplificando a nova função
Assim podemos calcular essa integral pelo método de integração polinomial, onde somamos no expoente da variável e dividimos a própria variável pelo resultado da soma do seu expoente...
Não podemos deixar o resultado em função de então temos que retornar para
E esse é o resultado da integral que tínhamos no enunciado!
Interessante, não é? 😁😁
Fim! Iae, o que achou? Responde Aí! 😁
