1b) Calcule
Passo 1
Ok, OK, admito, essa integral assusta um pouco. Mas relaxa que vamos tirar de letra, beleza? Primeiro, nota o seguinte. Termo ao quadrado somado com um número, dentro de uma raiz. Geralmente quando isso acontece, é uma boa ideia a gente tentar uma substituição trigonométrica. Montando então o seguinte triângulo auxiliar:
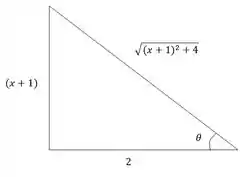
Podemos fazer a seguinte substituição trigonométrica:
Temos tudo agora pra achar uma expressão tanto pra quando pra . Pro primeiro, basta continuarmos olhando pro triângulo auxiliar:
E pra , basta a gente derivar em relação a a nossa substituição otrigonométrica:
Fazendo também a troca dos limites de integração, temos:
Passo 2
Belezinha, agora que sabemos:
Basta a gente substituir na integral:
O que dá em:
Terminando as contas pra partir pro abraço, temos:
Feshow!