Integração por Substituição Trigonométrica
Calcule as seguintes integrais
Passo 1
Não tem mistério! O enunciado nos pede para calcularmos uma integral indefinida. Ou seja, o resultado deve ser uma família de funções (Não esquecer da constante , marujo)!
Vamos começar tentando uma substituição. Sabemos que a derivada de é . Então, parece fazer sentido substituir .
Passo 2
Vamos começar usando a seguinte substituição:
Substituindo, teremos:
Percebemos que existe um termo do tipo . Esse é um indício de que teremos que usar o método de integração por substituição trigonométrica.
Passo 3
Agora, vamos seguir o passo a passo da integração por substituição trigonométrica:
1. Identificar o caso da substituição trigonométrica e o .
Devemos comparar o que a gente tem com esse cara aqui
Como temos o nosso é 1!
2. Aplicar a substituição recomendada e calcular .
Temos que fazer , logo
3. Substituir na integral dada.
Passo 4
4. Resolver a integral na variável .
5. Usar o triângulo retângulo para converter o na variável inicial.
Fizemos que
Sabemos que .
Assim, , ,
Vamos colocar na figurinha
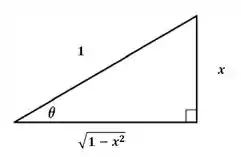
Logo, ( quer dizer o “arco” cujo seno é ).
Substituindo:
Acabou? Não! Lembra que a gente fez ?
Então, precisamos voltar para ! Ou seja
Finalmente,
Onde é uma constante.