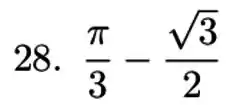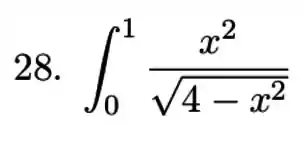
Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Substituição Trigonométrica

Ver Teoria
Exercício 501234567891011121314151617181920212223242526272829303132333435363738394041424344454647484951525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Passo 1

Esse caso tem cara de integração por substituição trigonométrica. Perceba que

4 - x 2

Está no mesmo formato que

a 2 - x 2

Então

a = 2

E nesse caso a substituição adequada é

x = 2 sen ⁡ θ

Passo 2

O próximo passo é derivar nosso x

x = 2 sen ⁡ θ

d x = 2 cos ⁡ θ d θ

E aplicar tudo na nossa integral

∫ x 2 4 - x 2 d x = ∫ 4 sen 2 ⁡ θ 4 - 4 sen 2 ⁡ θ 2 cos ⁡ θ d θ

Passo 3

Melhorando nossa expressão vamos ficar com

∫ x 2 4 - x 2 d x = ∫ 4 sen 2 ⁡ θ 4 ( 1 - sen 2 ⁡ θ ) 2 cos ⁡ θ d θ

Utilizando a identidade trigonométrica cos 2 ⁡ θ + sen 2 ⁡ θ = 1

∫ x 2 4 - x 2 d x = ∫ 4 sen 2 ⁡ θ 4 ( cos 2 ⁡ θ ) 2 cos ⁡ θ d θ

∫ x 2 4 - x 2 d x = ∫ 4 sen 2 ⁡ θ 2 cos ⁡ θ 2 cos ⁡ θ d θ

∫ x 2 4 - x 2 d x = ∫ 4 sen 2 ⁡ θ 2 cos ⁡ θ 2 cos ⁡ θ d θ

∫ x 2 4 - x 2 d x = 4 ∫ sen 2 ⁡ θ d θ

Passo 4

Para resolver essa integral, podemos lançar mão de outra identidade.

sen 2 ⁡ θ = 1 2 - cos ⁡ 2 θ 2

Então ficamos com

∫ x 2 4 - x 2 d x = 4 ∫ sen 2 ⁡ θ d θ

∫ x 2 4 - x 2 d x = 4 2 ∫ d θ - ∫ cos ⁡ ( 2 θ )   d θ

E resolvendo as integrais, nossa expressão será

∫ x 2 4 - x 2 d x = 2 θ - 2 sen ⁡ θ cos ⁡ θ

Passo 5

Agora temos que desfazer a substituição trigonométrica. Se pensarmos no triângulo retângulo.

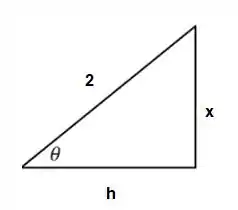
Podemos encontrar o outro cateto usando Pitágoras.

2 2 = x 2 + h 2

h = 4 - x 2

Daí temos que

sen ⁡ θ = x 2   , cos ⁡ θ = 4 - x 2 2 ,   θ = arcsen ⁡ x 2

Substituindo na expressão

∫ x 2 4 - x 2 d x = 2 θ - 2 sen ⁡ θ cos ⁡ θ

∫ x 2 4 - x 2 d x = 2 arcsen ⁡ x 2 - 2 x 2 4 - x 2 2

∫ x 2 4 - x 2 d x = 2 arcsen ⁡ x 2 - x 4 - x 2 2

Passo 6

Por fim, só falta aplicar os limites de integração

∫ 0 1 x 2 4 - x 2 d x = 2 arcsen ⁡ x 2 - 2 x 2 4 - x 2 2

∫ 0 1 x 2 4 - x 2 d x = 2 arcsen ⁡ 1 2 - 4 - 1 2 2 - 2 arcsen ⁡ 0 2 + 0

∫ 0 1 x 2 4 - x 2 d x = 2 π 6 - 3 2

∫ 0 1 x 2 4 - x 2 d x = π 3 - 3 2

Fim!

Resposta

Exercícios de Livros Relacionados

Encontre o volume do sólido obtido pela rotação em torno da reta x = 1 da região sob a curva y = 1 - x 2 , 0 ≤ x ≤ 1 .
Calcule a integral usando a substituição trigonométrica indicada. Esboce e coloque legendas no triângulo retângulo associado. ∫ x 3 9 - x 2 d x ; x = 3 sin ⁡ θ
Calcule a integral indefinida:int (x^2)/(sqrt(2 - x^2)) d x
Calcule a integral indefinida:int (5 x + 4)/(x^3 sqrt(x^2 + 1)) d x
Calcule a integralint (1)/(x^2 sqrt(4 x^2 - 1)) d x