Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Substituição Trigonométrica

Ver Teoria
Exercício 421234567891011121314151617181920212223242526272829303132333435363738394041434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Use substituição trigonométrica para calcular a integral dada:

∫ 2 x 3 1 - x 2 d x

Passo 1

Vamos resolver essa integral por substituição trigonométrica. Para começar, precisamos identificar em qual caso estamos. Temos

1 - x 2

Perceba que isso tem o formato

a 2 - x 2

Nesse caso podemos substituir x por

x = a sen ⁡ θ

Ou

x = a cos ⁡ θ

Vamos escolher x = a sen ⁡ θ ,   mas tanto faz ok? Então ficamos com

x = sen ⁡ θ

Passo 2

O segundo passo vai ser encontrar d x derivando o que determinamos para x

x = sen ⁡ θ

d x = cos ⁡ θ

Passo 3

Agora precisamos substituir x e d x na nossa integral

∫ 2 x 3 1 - x 2 d x = 2 ∫ x 3 1 - x 2 d x

2 ∫ x 3 1 - x 2 d x = 2 ∫ sen 3 ⁡ θ 1 - sen 2 ⁡ θ cos ⁡ θ   d θ

Sabemos que cos 2 ⁡ θ = 1 - sen 2 ⁡ θ então

2 ∫ x 3 1 - x 2 d x = 2 ∫ sen 3 ⁡ θ cos 2 ⁡ θ cos ⁡ θ   d θ = 2 ∫ sen 3 ⁡ θ cos ⁡ θ cos ⁡ θ   d θ

Cortando cos ⁡ θ em cima e em baixo, nos resta:

2 ∫ x 3 1 - x 2 d x = 2 ∫ sen 3 ⁡ θ   d θ

Passo 4

Falta resolver de fato a integral então olha só a sagacidade:

2 ∫ sen 3 ⁡ θ   d θ = 2 ∫ sen 2 ⁡ θ sen ⁡ θ   d θ

Como isso ajuda a gente? Bem, sabemos que sen 2 ⁡ θ = 1 - cos 2 ⁡ θ . Se fizermos então a substituição simples:

u = cos ⁡ θ

d u = - sen ⁡ θ   d θ

Podemos reescrever a integral para

2 ∫ sen 3 ⁡ θ   d θ = 2 ∫ sen 2 ⁡ θ sen ⁡ θ   d θ

2 ∫ sen 3 ⁡ θ   d θ = 2 ∫ 1 - cos 2 ⁡ θ sen ⁡ θ   d θ

2 ∫ sen 3 ⁡ θ   d θ = - 2 ∫ 1 - cos 2 ⁡ θ - sen ⁡ θ   d θ

E logo:

2 ∫ sen 3 ⁡ θ   d θ = - 2 ∫ 1 - u 2 d u

O que resolvemos e ficamos com:

2 ∫ sen 3 ⁡ θ   d θ = - 2 u - u 3 3

Vamos adicionar as constantes de integração só no final ok? Desfazendo a substituição temos

2 ∫ sen 3 ⁡ θ   d θ = - 2 cos ⁡ θ - cos 3 ⁡ θ 3

Então chegamos em

∫ 2 x 3 1 - x 2 d x = - 2 cos ⁡ θ - cos 3 ⁡ θ 3

Passo 5

Por fim, não podemos dar a resposta em função de θ   então precisamos voltar para o formato da função em x . Para isso vamos lembrar do triângulo retângulo. Temos que

x = sen ⁡ θ

Então sen ⁡ θ = x 1

Sabemos que

sen ⁡ θ = c a t e t o   o p o s t o h i p o t e n u s a

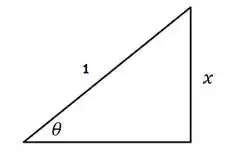
Vamos usar Pitágoras para encontrar o outro cateto

1 2 = x 2 + c a t 2

c a t = 1 - x 2

Então

cos ⁡ θ = 1 - x 2 1

cos ⁡ θ = 1 - x 2

Substituindo no resultado da integral

∫ 2 x 3 1 - x 2 d x = - 2 1 - x 2 - 1 - x 2 3 3

∫ 2 x 3 1 - x 2 d x = 2 3 1 - x 2 3 2 - 2 1 - x 2 + C

Resposta

∫ 2 x 3 1 - x 2 d x = 2 3 1 - x 2 3 2 - 2 1 - x 2 + C

Exercícios de Livros Relacionados

Encontre o volume do sólido obtido pela rotação em torno da reta x = 1 da região sob a curva y = 1 - x 2 , 0 ≤ x ≤ 1 .
Calcule a integral usando a substituição trigonométrica indicada. Esboce e coloque legendas no triângulo retângulo associado. ∫ x 3 9 - x 2 d x ; x = 3 sin ⁡ θ
Calcule a integral indefinida:int (x^2)/(sqrt(2 - x^2)) d x
Calcule a integral indefinida:int (5 x + 4)/(x^3 sqrt(x^2 + 1)) d x
Calcule a integralint (1)/(x^2 sqrt(4 x^2 - 1)) d x