Calcule as integrais:
g)
Passo 1
Fala, galera! Vamos resolver essa questão.
O enunciado pediu pra gente resolver a integral:
A primeira coisa que a gente pode pensar é em tentar usar substituição simples ou uma integração por partes, mas nenhuma delas vai ajudar a gente.

Repara que nós temos um denominador . Sempre que a gente tem algo desse tipo, nós podemos usar substituição trigonométrica.
Mas como é que a gente faz isso? No nosso caso, temos , e o nosso é o . Vamos considerar que esse seja sempre um número positivo. Beleza, mas se a gente precisa fazer uma substituição trigonométrica, qual substituição a gente pode fazer?
Cada caso é um caso, e pra cada um a gente tem um tipo de substituição diferente, olha só:
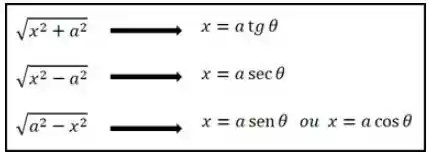
Como o nosso caso é o terceiro, a gente pode usar ou . Vamos escolher , como nosso e temos:
Agora achamos o , derivando o :
E substituímos na integral. Vamos lá!
Passo 2
Primeiro vamos olhar a substituição só na nossa raiz:
Nós sabemos que , então:
Substituindo na raiz:
Reparou que sumiu a raiz, né? Esse tipo de integração serve justamente pra tirar essa raiz, então fica atento a isso.
Antes de substituir tudo na integral, note que a nossa integral é definida. Então, precisamos arrumar também os limites de integração e ver o que acontece quando e quando .
Quando , da nossa substituição isolamos e temos:
Agora quando , temos:
Agora podemos arrumar tudo na integral.
Passo 3
Da nossa integral:
Temos:
Colocando a constante do lado de fora da integral:
Agora ficou mais de resolver do que aquela integral original, né? A gente só tem que manipular esse um pouquinho.
Passo 4
Nós podemos escrever . Assim,
Vamos nos lembrar de novo da identidade trigonométrica, , só que agora vamos isolar
Substituindo isso na integral:
Multiplicando por todo mundo nos parênteses:
Podemos separar isso em duas integrais, por integral da subtração é a subtração das integrais (lembra dessa propriedade?):
A integral do a gente sabe que é . E a integral de ? A gente pode resolver ela separadamente, usando uma substituição:
Achando , derivando:
Percebe que é justamente o termo que tá ali dentro da integral? Então, vamos substituir colocando o sinal negativo do lado de fora:
Voltando à nossa variável , que nós tínhamos substituído:
Agora, colocando tudo lá na nossa integral original, temos:
Aplicando os limites de integração:
Resolvendo dentro dos parênteses, temos:
Simplificando a fração por , temos:
Uffa! Encontramos nosso resultado. Valeu, galera! 😉