Calcular:
Passo 1
Uma raiz quadrada de um termo estranho no denominador? Toda a cara de uma integral por substituição trigonométrica. Esse caso, de acordo com a nossa teoria, é esse aqui:
Agora, repara que tem um detalho no termo da raiz:
Temos que deixar o sozinho para descobrir qual seria o e assim o :
Assim,
Passo 2
Vamos fazer a substituição e resolver:
Passo 3
Vamos usar aquele triângulo auxiliar para desfazer a substituição do . Temos que
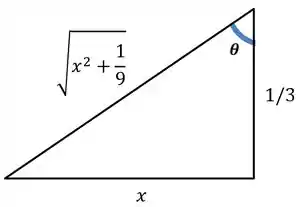
De acordo com essa figura, o valor de é:
Assim, o valor da integral será: