Seja um número real fixado. Calcule
Passo 1
E aí pessoal, tudo bem?
Essa questão parece complicada, mas vou ajudar você aqui! O problema pediu para calcularmos essa integral aqui
Mas por fora temos um limite! Então precisamos resolver essa integral que está por dentro, aplicar os limites de integração e depois, quando tivermos um resultado em função de , avaliar o limite quando

Mas relaxa que vou fazer passo a passo com você!
Passo 2
Primeiro vamos resolver essa integral:
Logo de cara vemos que tem uma função exponencial com um polinômio. Não temos a derivada de uma nem da outra no integrando, então não podemos usar a técnica da substituição simples. O que nos resta? POR PARTES!

Relembrando a técnica de integração...
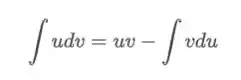
Mas qual função escolher para ? E para ? Se você não sabe qual escolher para , você pode usar o LIATE:

Assim vamos escolher e . Daí temos:
Agora é só substituir na fórmula de partes:
Beleza?
Passo 3
Agora vamos aplicar nos limites de integração:
Tranquilo até aqui?

Passo 4
Nosso passo final é calcular aquele limite!
Podemos separar em três limites:
- Calculando primeiro o limite mais à esquerda:
- Calculando o limite bem ao centro:
- Por fim o limite mais à direita:
Como têm-se uma indeterminação, vamos aplicar a regra de L’Hopital e avaliar novamente o limite (lembrando que vamos derivar essa coisa em M):
Beleza?

Agora vamos para o segundo limite:
Tudo bem?

Vamos para o último?
Nosso último passo é juntar todos os resultados:
E nossa integral fica:
E é isso!
Espero ter ajudado! Vamos para a próxima?