Um bloco de massa está preso a um eixo por uma corda ideal de tamanho . O bloco é solto com a corda esticada na posição horizontal.
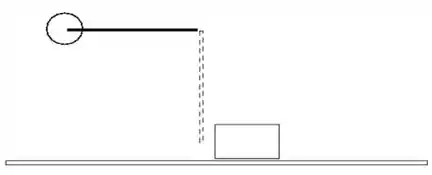
a) (0,5 pontos) Calcule a velocidade do bloco e a tração na corda no ponto mais baixo de sua trajetória;
b) (1,0 pontos) No ponto mais baixo de sua trajetória o bloco colide com um segundo bloco de massa , e recua com metade da sua velocidade. Calcule a velocidade que o bloco de massa adquire após a colisão, e a energia dissipada na colisão;
c) (1,0 pontos) Considerando que o coeficiente de atrito cinético entre o bloco de massa m e o chão é = 0,25, calcule a distância percorrida por este bloco até parar;
d) (0,5 pontos) Calcule o momento angular de cada bloco antes e depois da colisão (módulo, direção e sentido). Há conservação de momento angular? Justifique.
Passo 1
Essa questão é aquela questão completona, total flex. Ela quer que você demostre tudo que você sabe. Vamos começar então pela letra a), beleuza?
a)
Essa letra, nos pede a velocidade do bloco M e a tração na corda no ponto mais baixo. Vamos dar uma olhada no movimento que o bloco M faz antes de bater no bloco m, bora!
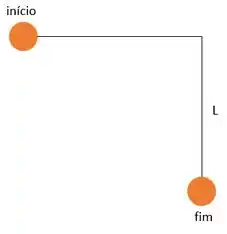
Conservando a energia mecânica desse sistema, teremos que:
E para descobrir o valor da tração no ponto mais baixo, vamos dar uma olhada no diagrama do corpo livre desse nosso peso aí.
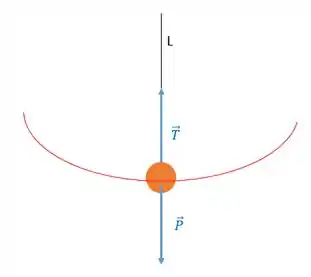
Olha só, esse pêndulo faz um movimento circular, e portanto podemos relacionar a força resultante que aponta para o centro do movimento como sendo a força centrípeta, certo?
Daí é só lembrar que essa força centrípeta tem uma fórmula para ela, e correr pro abraço.
Passo 2
b)
O-LHA A CO-LI-SÃO !!
Na letra b), pede para avaliar o que acontece com o bloco m após a colisão.
Primeiro, vamos dar uma olhada nessa colisão aí.
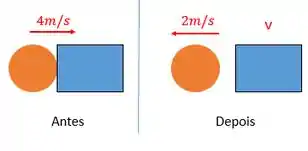
Lembrando de colisão, a gente vai puxar da memória que na colisão o momento se conserva, certo?
Tomando para direita positivo, como é de costume:
Agora só falta calcular a energia dissipada. E aí, como que a gente vai fazer isso ? Ué, calcule a energia no início, calcula a energia no final, a diferença de uma pra outra, é a energia que foi dissipada.
Logo, a energia dissipada é:
Passo 3
Eu disse que essa questão é do tipo completona né, olha só:
c)
Nessa letra, ele pede para você indicar quanto que o bloco vai percorrer, sendo que uma força de atrito está agindo sobre ele.
Então, você sabe que a velocidade inicial do bloco é , certo?
E o valor dessa força de atrito pode ser encontrado:
Agora, pensa só, essa força de atrito realiza um trabalho negativo no bloco, certo?
E esse trabalho, nada mais é do que a variação de energia do bloco.
Passo 4
Vamos lá, falta pouco agora:
d)
Vamos calcular o momento angular de cada um dos nossos corpos. Antes e depois da colisão.
Bloco de massa M
Mas temos que encontrar a direção e sentido desse momento angular aí.
Para isso, vamos usar a regra da mão-direita. Dá uma olhada no desenho:
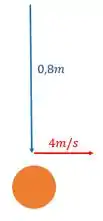
Pega sua mão, coloca os dedos na direção do vetor raio. Agora coloca a palma da mão na direção da velocidade. Fez isso tudo. Fecha a mão e vê para onde o seu polegar está apontando.
Ele tá apontando para fora da página, não tá ?
Fazendo a mesma coisa, só que agora com a velocidade de 2m/s, para a esquerda, você vai encontrar:
Agora, bora fazer isso tudo com o corpo de massa m, para acabar com essa bendita questãozinha.
Bloco de massa m
Ele sai do repouso, logo:
Após a colisão, nós temos a seguinte situation:
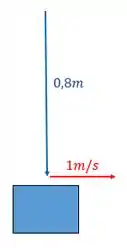
Aplicando os valores na equação e fazendo a regra da mão direta, você vai ter?
Então, agora, vamos ver o momento desse sistema se conserva:
Ok, vimos então que?
E a justificativa?
É simples, como não há a presença de torques externos ao sistema, o momento angular do sistema se conserva.
Resposta
a)
b)
c)
d) massa M:
massa m: 0, = 0,96 (saindo da página)
Os momentos se conservam, pois não torques externos ao sistema.