[ENUNCIADO COMUM ÀS QUESTÕES 3 E 4]
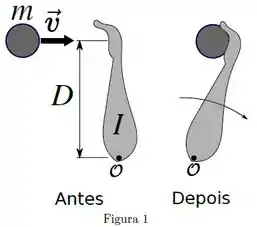
Uma pessoa possui um braço de momento de inércia e agarra uma bola de massa e velocidade inicial perpendicular ao braço. A bola é agarrada no instante a uma distância do ponto , como mostra a Figura 1. Imediatamente após receptar a bola, o sistema braço + bola gira em torno de um eixo que passa perpendicularmente ao ponto com velocidade angular . Considere que todo o movimento ocorre em um plano horizontal e que a gravidade não é relevante para a situação descrita.
[QUESTÃO 3]
Considere as afirmativas abaixo:
- O momento angular da bola em relação ao ponto não varia em .
- A energia mecânica do sistema não varia em .
- O momento angular do sistema em relação ao ponto não varia em .
Marque a alternativa que contém apenas afirmativa(s) verdadeira(s).
(a)
(b)
(c)
(d) e
(e) e
(f) e
(g) Todas
(h) Nenhuma
Passo 1
Temos um exemplo clássico sobre o conceito de momento angular.
Um objeto que andava linearmente e colide com o braço, entrando num movimento de rotação com ele.

Vamos tentar fazer um paralelo com uma colisão sem rotação...
Quando dois bloquinhos colidem sem a ação de forças externas:

O momento linear do sistema se conserva:
Já na colisão com rotação, observamos que isso ocorre com o momento angular...
Se não há a ação de torques externos, o momento angular do sistema se conserva:
Vamos às alternativas (começando com a e ).
Passo 2
- O momento angular da bola em relação ao ponto não varia em .
- O momento angular do sistema em relação ao ponto não varia em .
Temos que tomar muito cuidado na hora de considerar o nosso sistema!
Quando falamos que não há torque externo, isso não significa que não há forças e torques dentro do sistema.
Quando a bola colide com o braço, existe uma força que a bola exerce sobre o braço e, pela ação e reação, uma força que o braço exerce sobre a bola:
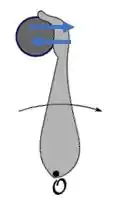
Porém, essas forças são de mesmo módulo e sentidos opostos.
Elas se anulam... por isso, chamamos de forças internas quando estamos considerando um sistema bola+braço.
Assim, os torques das duas forças também se anulam (torques internos) e não há torque resultante nesse mesmo sistema bola+braço:
Logo o momento angular do sistema bola+braço se conserva:
A afirmativa é verdadeira!
Porémmmmmmmm...
Quando falamos do momento angular da bola (afirmativa ), a coisa muda um pouco.
Agora, o nosso sistema é apenas a bola.
Ou seja, a força que o braço exerce sobre a bola é uma força externa e o torque gerado por essa força é um torque externo:

Assim, o momento angular da bola não se conserva.
A afirmativa é falsa.
A ideia é que o momento angular da bola diminui com a colisão e o momento angular do braço aumenta com a colisão, de forma que a soma dos dois (sistema bola+braço) continue com o mesmo momento angular .
Passo 3
- A energia mecânica do sistema não varia em .
Essa afirmativa está incorreta!
A bola e o braço colidem inelásticamente, ou seja, elas saem juntas da colisão.
Numa colisão inelástica, não há a conservação de energia cinética, portanto a energia mecânica do sistema não se conserva.
Se fosse preciso provar isso, poderíamos calcular a velocidade inicial da bolinha para achar sua enegria cinética inicial e com isso, comparamos com a energia cinética de rotação da bola+braço após a colisão para mostrar que são diferentes. Porém, acredito que a saída a partir da ideia seja mais tranquila para essa múltipla-escolha.
A ideia é a mesma para os bloquinhos que colidem inelásticamente:
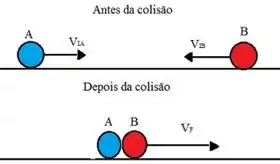
A grandeza que sempre se conserva é o momento linear (numa colisão isolada):
Porém a energia cinética não se conserva.
No caso da bola e do braço:
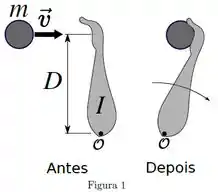
O que se conerva é o momento angular:
Porém a energia cinética não se conserva:
Resposta
Letra (c)